Need some help with this assignment

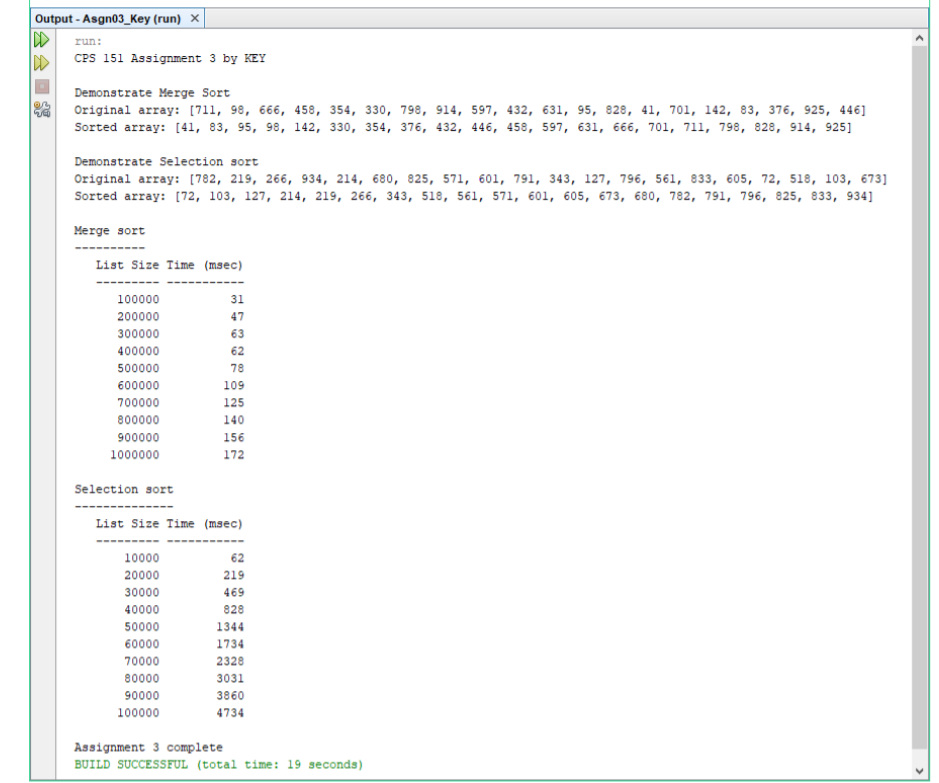
We discussed in class how Merge Sort is more efficient than Selection sort (O(n log n) vs. O(n2 )). In this assignment you are asked to run the two algorithms on random arrays of different sizes and produce a table of running times. You can use the codes for the two techniques posted on Isidore or use the code from the textbook. In your program put a comment to show whether you are using the book's sorting code or the code from Isidore. You are welcome to write your own code as well. The program should have two output sections. In the first section you create random arrays of size 20 (limit values to 100), and demonstrate that selection sort and merge sort as implemented by you work to sort the array. In the second section you collect timing data from sorting random arrays of various sizes using both selection sort and merge sort and display the results in a table. See sample output. When running this program to collect final results for submission, close all other applications. For collecting timing data, use rand.nextInt(), without using any specified range. These are the results I got from my program. Different runs do tend to give different results.

Here is the code provided for each type of sorting method:

 package mergesort; import static java.lang.System.arraycopy; import static java.lang.System.out; import java.util.Arrays; import java.util.Random; /** * * @author anon */ public class MergeSort { final static Random rand = new Random(); /** * @param args the command line arguments */ public static void main(String[] args) { // TODO code application logic here int[] arr = new int[8]; for (int j = 0; j  1 // Consider arr[low:high] split into arr[low:mid] and arr[mid+1:high] // and sort them recursively where mid = (low + high) / 2 final int mid = (low + high) / 2; sort(arr, low, mid, level + 1); sort(arr, mid + 1, high, level + 1); // merge arr[low:mid] and arr[mid+1:high] into arr[low:mid] merge(arr, low, high, level); } // end private sort private static void merge(final int[] arr, final int low, final int high, int level) { // array segment arr[low:high] contains two sorted subsegments arr[low:mid] // and arr[mid+1:high] where mid = (low + high) / 2 final int mid = (low + high) / 2; // temporary array into which the segments arr[low:mid] and arr[mid+1:high] // are merged. The size needed is high - low + 1 final int[] tempArr = new int[high - low + 1]; // index variables set into segments to merge and into the tempArray int index1 = low, index2 = mid + 1, index3 = 0; indent(level); out.println("Merging " + segmentToString(arr, low, mid) + " and " + segmentToString(arr, mid + 1, high)); while (index1  high) return "[]"; // at least one value String str = "[" + arr[low]; for (int index = low + 1; index  
Selection Sort:
 
package selectsort; import static java.lang.System.out; import java.util.Arrays; /** * * @author anon */ public class SelectSort { /** * @param args the command line arguments */ public static void main(String[] args) { // TODO code application logic here int[] arr = {89, 17, 45, 78, 65, 23, 56, 19, 31, 29}; out.println("Original array: " + Arrays.toString(arr)); sort(arr); out.println(" Sorted array: " + Arrays.toString(arr)); } // end main private static void sort(int[] arr) { final int n = arr.length; // size of array for (int k = 0; k   Output-Asgn03-Key (run)  run: CPS 151 Assignment 3 by kEY Demonstrate Merge Sort riginal array: [711, 98, 666, 458, 354, 330, 798, 914, 597, 432, 631, 95, 828, 41, 701, 142, 83, 376, 925, 446] Sorted array: [41, 83, 95, 98, 142, 330, 354, 376, 432, 446, 458, 597, 631, 666, 701, 711, 798, 828, 914, 925] Demonstrate Selection sort Original array: [782, 219, 266, 934, 214, 680, 825, 571, 601, 791, 343, 127, 796, 561, 833, 605, 72, 518, 103, 673] Sorted array: [72, 103, 127, 214, 219, 266, 343, 518, 561, 571, 601, 605, 673, 680, 782, 791, 796, 825, 833, 934] Merge sort List Size Time (msec) 100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 31 47 63 62 78 109 125 140 156 172 Selection sort List Size Time (msec) 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000 62 219 469 828 1344 1734 2328 3031 3860 4734 Assignment 3 complete BUILD SUCCESSFUL (total time: 19 seconds)  Output-Asgn03-Key (run)  run: CPS 151 Assignment 3 by kEY Demonstrate Merge Sort riginal array: [711, 98, 666, 458, 354, 330, 798, 914, 597, 432, 631, 95, 828, 41, 701, 142, 83, 376, 925, 446] Sorted array: [41, 83, 95, 98, 142, 330, 354, 376, 432, 446, 458, 597, 631, 666, 701, 711, 798, 828, 914, 925] Demonstrate Selection sort Original array: [782, 219, 266, 934, 214, 680, 825, 571, 601, 791, 343, 127, 796, 561, 833, 605, 72, 518, 103, 673] Sorted array: [72, 103, 127, 214, 219, 266, 343, 518, 561, 571, 601, 605, 673, 680, 782, 791, 796, 825, 833, 934] Merge sort List Size Time (msec) 100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 31 47 63 62 78 109 125 140 156 172 Selection sort List Size Time (msec) 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000 62 219 469 828 1344 1734 2328 3031 3860 4734 Assignment 3 complete BUILD SUCCESSFUL (total time: 19 seconds)