No more information to add.

ignore part b in the previous screenshot.

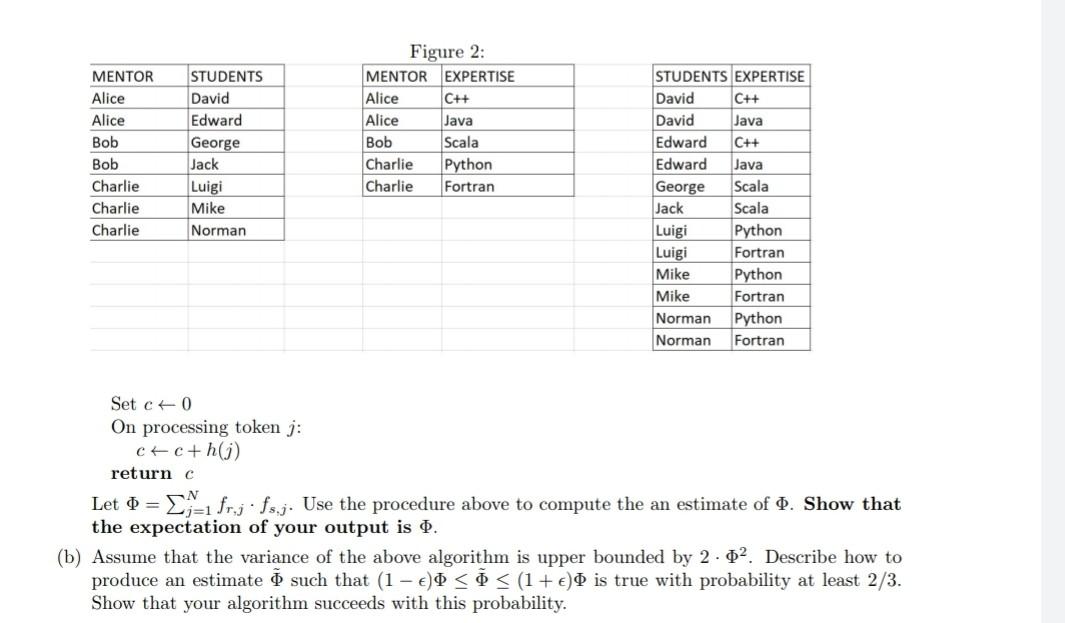
(3 points) In the lecture, we noted that F2 represents the size of a self-join of the same table. In this problem, you will generalize the algorithm to compute the estimate of the size of the join between two different tables. For two relations (i.e. tables in a database) r(A, B) and s(A,C), with a common attribute (i.e.,column) A, we define the join r xs to be a relation consisting of all tuples (a,b,c) such that (a,b) er and (a,c) s. Therefore, if fr.j and fs.j denote the frequencies of j in the first columns (i.e., A-columns) of r and s, respectively, and j can take values in {1,...,N}, then the size of join is D-1 fr.j fs.j. For example, in Figure 2, the third table is the join of the first two tables, joined by the key "MENTOR. The size (# rows) of the table is 2 x 2 + 2 x 1+3 x 2 = 12. Suppose that the first table and the second table are given as streams 01 and 02 respectively. (You may ignore irrelevant information outside of the first column and assume that each item in the stream is a single token ;). (a) Consider the following procedure: Choose a hash function h from a 4-universal hash family that map (1,N] to {-1, +1}. Consider the following sketching algo- rithm: procedure fo, h) (b) To get a running time that is sublinear in N, we need to do the query more efficiently. Assume that N is a power of 2. Define the Dyadic intervals as follows: Lo = {{1}, {2},...,{N}} = {{1,2},{3, 4},...,{N 1, N}} L2 = {{1,2,3,4}, {5,6,7,8},...,{N - 3, N - 2, N -1,N}} 2/3 Lig N = {{1, 2, ...,N}} Note that if [i,j] is an interval in Lk for k > 0, then it must be the case that (i,(i+j)/2], [(i + j)/2+1, j) are intervals in Lx-1. We call these intervals the children intervals of [i,j]. Conversely, [i, j] is the parent of these two intervals. We construct 1+lg N Count-Min Sketches with e=1/6 and 8 = 1/6N), one for each Lk, to sketch the frequency for every I E Lx (the frequency of an interval refers to the sum of the frequency of the items in the interval). At the end of the stream, we run the following recursive procedure that queries the intervals in a depth-first search manner. We will begin by calling Query([1, N],lg N). procedure Query(Interval I, level) if level = 0 then Report the element belonging to the singleton interval I end if Let I1, I2 be the children intervals of I. Get estimates on the frequencies of 11 and 12. Let fi, and fi, be the estimates. if f1 > F1/3 then Execute Query(I, level - 1) recursively. end if if fiz > F1/3 then Execute Query(12, level-1) recursively. end if Let & be the event that for all 0 Sk 2/3. Then, show that if Eholds, the algorithm uses at most O(log N) queries and it solves the problem. Remarks. In (strict) turnstile streams, it is important to distinguish between n and F1. Here, F1 is the total counts of the elements at the end of the stream, while n is maximum total counts of the elements over any given time during the stream. Also, the update sequence can be arbitrarily long, so the error probability can cumulate if we were to do a query after each update. This rules out the approach of maintaining the top 6 frequent items using a heap. MENTOR Alice Alice Bob Bob Charlie Charlie Charlie STUDENTS David Edward George Jack Luigi Mike Norman Figure 2: MENTOR EXPERTISE Alice C++ Alice Java Bob Scala Charlie Python Charlie Fortran STUDENTS EXPERTISE David C++ David Java Edward C++ Edward Java George Scala Jack Scala Luigi Python Luigi Fortran Mike Python Mike Fortran Norman Python Norman Fortran Set c0 On processing token j: C+ C+h() return c Let 0 = [-1.fr,j. fs.j. Use the procedure above to compute the an estimate of . Show that the expectation of your output is . (b) Assume that the variance of the above algorithm is upper bounded by 2. 02. Describe how to produce an estimate such that (1 - e) 0, then it must be the case that (i,(i+j)/2], [(i + j)/2+1, j) are intervals in Lx-1. We call these intervals the children intervals of [i,j]. Conversely, [i, j] is the parent of these two intervals. We construct 1+lg N Count-Min Sketches with e=1/6 and 8 = 1/6N), one for each Lk, to sketch the frequency for every I E Lx (the frequency of an interval refers to the sum of the frequency of the items in the interval). At the end of the stream, we run the following recursive procedure that queries the intervals in a depth-first search manner. We will begin by calling Query([1, N],lg N). procedure Query(Interval I, level) if level = 0 then Report the element belonging to the singleton interval I end if Let I1, I2 be the children intervals of I. Get estimates on the frequencies of 11 and 12. Let fi, and fi, be the estimates. if f1 > F1/3 then Execute Query(I, level - 1) recursively. end if if fiz > F1/3 then Execute Query(12, level-1) recursively. end if Let & be the event that for all 0 Sk 2/3. Then, show that if Eholds, the algorithm uses at most O(log N) queries and it solves the problem. Remarks. In (strict) turnstile streams, it is important to distinguish between n and F1. Here, F1 is the total counts of the elements at the end of the stream, while n is maximum total counts of the elements over any given time during the stream. Also, the update sequence can be arbitrarily long, so the error probability can cumulate if we were to do a query after each update. This rules out the approach of maintaining the top 6 frequent items using a heap. MENTOR Alice Alice Bob Bob Charlie Charlie Charlie STUDENTS David Edward George Jack Luigi Mike Norman Figure 2: MENTOR EXPERTISE Alice C++ Alice Java Bob Scala Charlie Python Charlie Fortran STUDENTS EXPERTISE David C++ David Java Edward C++ Edward Java George Scala Jack Scala Luigi Python Luigi Fortran Mike Python Mike Fortran Norman Python Norman Fortran Set c0 On processing token j: C+ C+h() return c Let 0 = [-1.fr,j. fs.j. Use the procedure above to compute the an estimate of . Show that the expectation of your output is . (b) Assume that the variance of the above algorithm is upper bounded by 2. 02. Describe how to produce an estimate such that (1 - e)