numerical method hw and requirement thank u

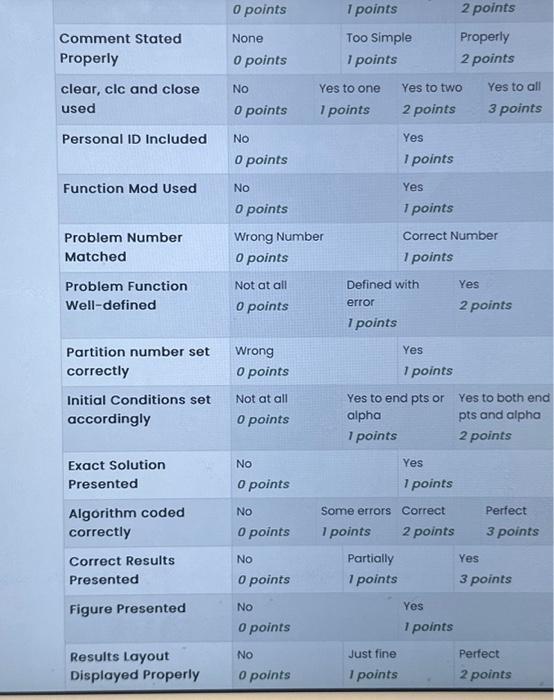
num of question =mod(ID,8)+1 You should check the function, mod, first in order to get familiar with this command cause we will need to use it for future homework frequently. a. y=te2x2y,0t1.y(0)=0, with h=0.5; actual solution y(t)=31te3t21e3r+ 81e2i. b. y=1+(ty)2,2t3.y(2)=1, with h=0.5; actual solution y(t)=t+tt1. c. y=1+y/t,1t2,y(1)=2, with h=0.25; actual solution y(t)=tlnt+2t. d. y=cos2t+sin3t,0t1,y(0)=1. with h=0.25; actual solution y(t)= 21sin2t31cos3t+34. e. y=et,0t1,y(0)=1, with h=0.5; actual solution y(t)=ln(et+e1). f. y=1+y1+t,1t2,y(1)=2, with h=0.5; actual solution y(t)=t2+2t+61. g. y=y+ty1/2,2t3,y(2)=2. with h=0.25; actual solution y(t)= (t2+2eet/2)2 h. y=t2(sin2t2ty),1t2,y(1)=2, with h=0.25; actual solution y(t)= 21r2(4+cos2cos2t). Note: 1. Name your file in the format hw4_ID.m 2. After finishing, share your Octave online bucket and paste the link in the Comment field 3. State your comment or feeling about doing this homework in the comment field 4. Attached both the PDF file and m file of your code upon submission \begin{tabular}{|c|c|c|c|c|} \hline & 0 points & \multicolumn{2}{|l|}{ I points } & 2 points \\ \hline \begin{tabular}{l} Comment Stated \\ Properly \end{tabular} & \begin{tabular}{l} None \\ o points \end{tabular} & \begin{tabular}{l} Too Simp \\ I points \end{tabular} & & \begin{tabular}{l} Properly \\ 2 points \end{tabular} \\ \hline \begin{tabular}{l} clear, clc and close \\ used \end{tabular} & \begin{tabular}{l} No \\ opoints \end{tabular} & \begin{tabular}{l} Yes to one \\ lpoints \end{tabular} & \begin{tabular}{l} Yes to two \\ 2 points \end{tabular} & \begin{tabular}{l} Yes to all \\ 3 points \end{tabular} \\ \hline Personal ID Included & \begin{tabular}{l} No \\ opoints \end{tabular} & & \begin{tabular}{l} Yes \\ l points \end{tabular} & \\ \hline Function Mod Used & \begin{tabular}{l} No \\ opoints \end{tabular} & & \begin{tabular}{l} Yes \\ I points \end{tabular} & \\ \hline \begin{tabular}{l} Problem Number \\ Matched \end{tabular} & \begin{tabular}{l} Wrong Number \\ opoints \end{tabular} & & \begin{tabular}{l} Correct N \\ l points \end{tabular} & Number \\ \hline \begin{tabular}{l} Problem Function \\ Well-defined \end{tabular} & \begin{tabular}{l} Not at all \\ opoints \end{tabular} & \begin{tabular}{l} Defined v \\ error \\ 1 points \end{tabular} & with & \begin{tabular}{l} Yes \\ 2 points \end{tabular} \\ \hline \begin{tabular}{l} Partition number set \\ correctly \end{tabular} & \begin{tabular}{l} Wrong \\ opoints \end{tabular} & & \begin{tabular}{l} Yes \\ Ipoints \end{tabular} & \\ \hline \begin{tabular}{l} Initial Conditions set \\ accordingly \end{tabular} & \begin{tabular}{l} Not at all \\ o points \end{tabular} & \begin{tabular}{l} Yes to en \\ alpha \\ l points \end{tabular} & d pts or & \begin{tabular}{l} Yes to both end \\ pts and alpha \\ 2 points \end{tabular} \\ \hline \begin{tabular}{l} Exact Solution \\ Presented \end{tabular} & \begin{tabular}{l} No \\ o points \end{tabular} & & \begin{tabular}{l} Yes \\ lpoints \end{tabular} & \\ \hline \begin{tabular}{l} Algorithm coded \\ correctly \end{tabular} & \begin{tabular}{l} No \\ o points \end{tabular} & \begin{tabular}{l} Some errors \\ lpoints \end{tabular} & \begin{tabular}{l} Correct \\ 2 points \end{tabular} & \begin{tabular}{l} Perfect \\ 3 points \end{tabular} \\ \hline \begin{tabular}{l} Correct Results \\ Presented \end{tabular} & \begin{tabular}{l} No \\ o points \end{tabular} & \begin{tabular}{l} Partially \\ I points \end{tabular} & & \begin{tabular}{l} Yes \\ 3 points \end{tabular} \\ \hline Figure Presented & \begin{tabular}{l} No \\ o points \end{tabular} & & \begin{tabular}{l} Yes \\ I points \end{tabular} & \\ \hline \begin{tabular}{l} Results Layout \\ Displayed Properly \end{tabular} & \begin{tabular}{l} No \\ o points \end{tabular} & \begin{tabular}{l} Just fine \\ I points \end{tabular} & & \begin{tabular}{l} Perfect \\ 2 points \end{tabular} \\ \hline \end{tabular}