Please assist with answering and interpreting the following questions in the simplest way. I understand the Probability Distribution Normal Curve, and I understand how to obtain the z-scores and where the information may land on the normal curve, however, understanding how to word and apply the math to the questions asked seems difficult. please assist.

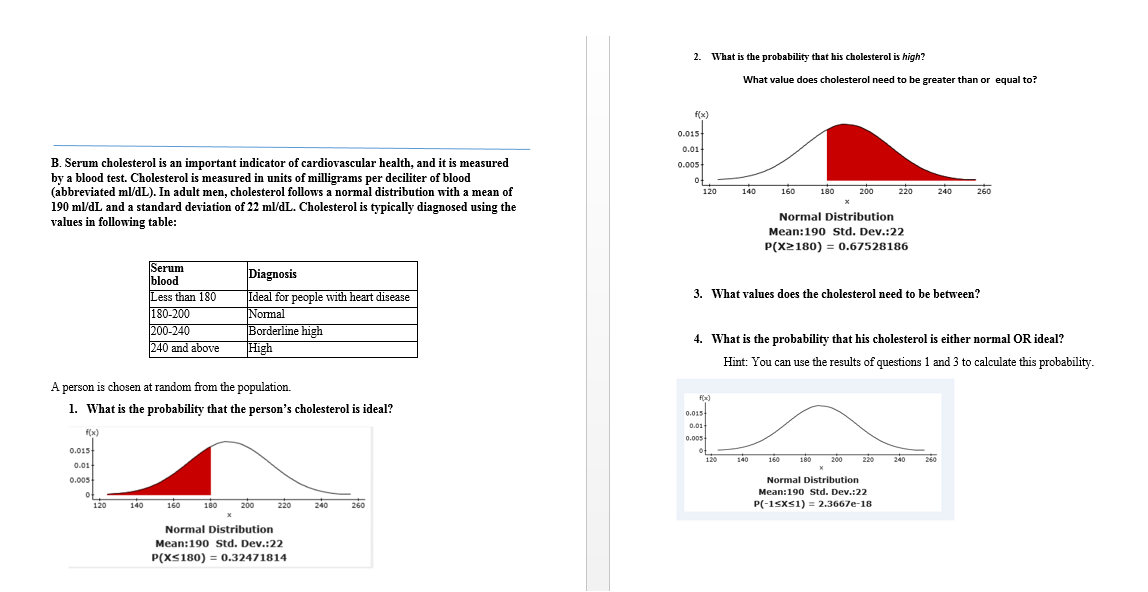
\fIntroductory Statistics: Exploring the World through Data ill'll'l 't 66 eQ MAT105 Summer || 2017 Herz... | excelsior00057 w- Summary Random samples or random experiments must be generated with the use of outside mechanisms such as computer algorithms or by relying on random number tables. Human intuition cannot be relied on to produce reliable \"randomness.\" Probability is based on the concept of long-run relative frequen- cies: If an action is repeated infinitely many times, how often does a particular event occur? To nd theoretical probabilities, we calculate these relative frequencies on the basis of assumptions about the situa- tion and rely on mathematical rules. In nding empirical probabilities, we actually carry out the action many times or, alternatively, rely on a simulation (using a computer or random number table) to quickly carry out the action many times. The empirical probability is the pro- portion of times a particular event was observed to occur. The Law of Large Numbers tells us that the empirical probability becomes closer to the true probability as the number of repetitions is increased. Theoretical Probability Rules Rule 1: A probability is always a number from 0 to l (or 0% to 100%) inclusive (which means 0 and 1 are allowed). It may be expressed as a fraction, a decimal, or a percent. 0 s P(A) s 1 Rule 2: For any event A, P(A does not occur) = 1 - P(A does occur) Sources Ac is the complement of A: P(AC) = 1 P(A) Rule 3: For equally likely outcomes: Number of outcomes in A p A = ( ) Number of all possible outcomes Rule 4: Always: P(A OR B) = P(A) + P(B) P(A AND B) Rule 43: Only if A and B are mutually exclusive: P(A OR B) = P(A) + P(B) Rule 53: Conditional probabilities P(A AND B) Probability of A given that B occurred: P(AIB) = P(B) Rule 51'): Always: P(A AND B) = P(B) P(A I B) Rule 5c: Multiplication Rule. If A and B are independent events, then P(A AND B) = P(A) P(B) This applies for any (finite) number of events. For example, P(A AND B AND C AND D) = P(A) P(B) P(C) P(D) if A, B, C, D are independent of each other. MetLife Survey of the American Teacher, 2009, http://www.harrisinteractive .corn Starr, Norton (1997), \"Nonrandorn Risk: The 1970 Draft Lottery," Journal of Statistics Education, volume 5, number 2. Vietnam-era draft data can be found, along with supporting references, at www.arnstat.org/ publications/j se/datasets/draft.txt. Pew Foundation, Social Media and Young Adults report, http://pewinternet .org (accessed July 2010). Introductory Statistics: Exploring the Worid through Data MAT'IOS Summer || 2017 Herz... l excelsior00057 ilIIII t. ea c O. a C?) {9 5.3 ASSOCIATIONS IN CATEGORICAL VARIABLES CHAPTER .5 b. This statement is also a conditional probability. c. This statement, on the other hand, is asking us to assume nothing and, instead, once the person is selected from the entire United States, to determine whether that per- son has these two characteristics. Using probability notation, these statements are a. P(person goes online I person is teenager) b. P(person goes online I person is adult aged 65 or older) C. P(person goes online AND person is teenager) TRY THIS! Exercise 5.45 Finding Conditional Probabilities If you are given a table like Table 5.5, you can nd conditional probabilities as we did above: by isolating the group from which you are sampling. However, a formula exists that is useful for times when you do not have such complete information. The formula for calculating conditional probabilities is P(A AND B) P(A|B) = P(B) EXAMPLE 10 Education and Marital Status Suppose a person is randomly selected from those represented in Table 5.3 on page 204. Find the probability that a person with less than a high school degree (and no higher degrees) is married. Use the table, but then confirm your calculation with the formula. We are asked to nd P(married | less than high school degree)in other words, the probability a person with less than a HS degree is married. We are told to imagine taking a random sample from only those who have less than a high school degree. There are 125 such people, of whom 70 are married. P(married|less HS) = 70/ 125 = 0.560 The formula conrms this: 70 _ P married AND less HS 665 70 P(marr1ed|less HS) = W = E = E = 0.560 E Interestingly, the probability that a college graduate is married (0.685) is greater than the probability that someone with less than a high school education is married (0.560). TRY THIS! Exercise 5.47 With a little algebra, we can discover that this formula can serve as another way of nding AND probabilities: P(A AND B) = P(A)P(B |A) We'll make use of this formula later. Introductory Statistics: Expioring the Worid through Data MAT'IOS Summer || 2017 Herz... l exceisior00057 iiIII i. 66 e O. a C?) {9 5. 3 ASSOCIATIONS IN CATEGORICAL VARIABLES CHAPTER .5 SECTION 5.3 Associations in Categorical Variables Judging on the basis of our sample in Table 5.3, is there an association between mari- tal status and having a college education? If so, we would expect the proportion of married people to be different for those who had a college education and those who did not have a college education. (Perhaps we would find different proportions of mar- ital status for each category of education.) In other words, if there is an association, we would expect the probability that a randomly selected college-educated person is married to be different from the probabil- ity that a person with less than a college education is married. Conditional Probabilities Language is important here. The probability that \"a college-educated person is mar- rie \" is different from the probability that \"a person is college-educated AND is mar- rie .\" In the AND case, we're looking at everyone in the sample and wondering how many have both a college degree AND are married. But when we ask for the probabil- ity that a college-educated person is married, we're taking it as given that the person is college-educated. We're not saying \"choose someone from the whole collection.\" We're saying, \"Just focus on the people with the college degrees. What proportion of those people are married?\" Probabilities such as these, where we focus on just one group of objects and imagine taking a random sample from that group alone, are called conditional probabilities. For example, in Table 5.5 (which repeats Table 5.3), we've highlighted in red the people with college degrees. In this row, there are 143 people. If we select someone at random from among those 143 people, the probability that the person will be married is 98/143 (or about 0.685). We call this a conditional probability because we're nding the probability of being married conditioned on having a college education (that is, we are assuming we're selecting only from college-educated people). ability that a person With a college Less HS degree or higher is married? To nd this. focus on the row shown in HS 68 240 59 30 397 red and imagine selecting a person College or higher 27' 98 15 3 143 from this row. Total 1 12 403 34 61 665 \"Given That\" vs. \"AND\" Often, conditional probabilities are worded with the phrase given that, as in \"Find the probability that a randomly selected person is married given that the person has a college degree.\" But you might also see it phrased as in the last paragraph: \"Find the probability that a randomly selected person with a college degree is married.\" The latter phrasing is more subtle, because it implies that we're supposed to assume the selected person has a college degree: We must assume we are given that the person has a college degree. Figure 5.6a on the next page shows a Venn diagram representing all of the data. The green overlap region represents the event of being married AND having completed col- lege. By way of contrast, Figure 5.6b on the next page shows only those with college edu- cations; it emphasizes that if we wish to find the probability of being married, given that the person has a college degree, we need to focus on only those with college degrees. Introductory Statistics: Exploring the World through Data ill'll'l 't 66 eQ MAT105 Summer || 2017 Herz... | excelsior00057 w- Summary Random samples or random experiments must be generated with the use of outside mechanisms such as computer algorithms or by relying on random number tables. Human intuition cannot be relied on to produce reliable \"randomness.\" Probability is based on the concept of long-run relative frequen- cies: If an action is repeated infinitely many times, how often does a particular event occur? To nd theoretical probabilities, we calculate these relative frequencies on the basis of assumptions about the situa- tion and rely on mathematical rules. In nding empirical probabilities, we actually carry out the action many times or, alternatively, rely on a simulation (using a computer or random number table) to quickly carry out the action many times. The empirical probability is the pro- portion of times a particular event was observed to occur. The Law of Large Numbers tells us that the empirical probability becomes closer to the true probability as the number of repetitions is increased. Theoretical Probability Rules Rule 1: A probability is always a number from 0 to l (or 0% to 100%) inclusive (which means 0 and 1 are allowed). It may be expressed as a fraction, a decimal, or a percent. 0 s P(A) s 1 Rule 2: For any event A, P(A does not occur) = 1 - P(A does occur) Sources Ac is the complement of A: P(AC) = 1 P(A) Rule 3: For equally likely outcomes: Number of outcomes in A p A = ( ) Number of all possible outcomes Rule 4: Always: P(A OR B) = P(A) + P(B) P(A AND B) Rule 43: Only if A and B are mutually exclusive: P(A OR B) = P(A) + P(B) Rule 53: Conditional probabilities P(A AND B) Probability of A given that B occurred: P(AIB) = P(B) Rule 51'): Always: P(A AND B) = P(B) P(A I B) Rule 5c: Multiplication Rule. If A and B are independent events, then P(A AND B) = P(A) P(B) This applies for any (finite) number of events. For example, P(A AND B AND C AND D) = P(A) P(B) P(C) P(D) if A, B, C, D are independent of each other. MetLife Survey of the American Teacher, 2009, http://www.harrisinteractive .corn Starr, Norton (1997), \"Nonrandorn Risk: The 1970 Draft Lottery," Journal of Statistics Education, volume 5, number 2. Vietnam-era draft data can be found, along with supporting references, at www.arnstat.org/ publications/j se/datasets/draft.txt. Pew Foundation, Social Media and Young Adults report, http://pewinternet .org (accessed July 2010). 10:38 AM 1 0 called the specificity of the test. Based on your answers to questions 3 and 4: 5. If a student has cheated, what is the probability that the test will return a negative result? (That is, the test incorrectly concludes the student did not cheat.) This is called the false negative rate of the test. If a student not cheated, what is the probability that the test will return a positive test result? (That is, the test incorrectly concludes that the student cheated.) This is called the false positive rate of the test. Calculating with probability Use the rules of conditional probability to answer the following questions. Show or explain your work for all calculations. (Hint: look at the example on page 235 of your text). 7. What is the probability that a randomlychosen student cheat and gets a positive result (the test correctly says that the student cheated)? 8. What is the probability that a randomlychosen student did n_ot cheat and gets a negative result (the test correctly says that the student did not cheat)? Page 2 of 3 9. Based on your responses to questions 7 and 8, what is the probability that the lie detector test results are correct? 10. What do you think about the accuracy of this test? Would you trust its results? 90% l:l- 1of3 10:38 AM The principal at Clarkstown High School suspects there has widespread cheating, and decides to require all students to take a lie detector test to see if they have cheated. Although the principal does not know this, 10% of the students have cheated. Interpreting probabilities A student is chosen at random from the school: 1. What is the probability that the student has cheated? 2. What is the probability that student has not cheated? The lie detector test result is called positive if it concludes that the person has cheated, and is called negative if it concludes the person has not cheated. However, the test is not perfectly accurate: 3. If a student has cheated, the probability that the test will return a positive result is 0.85. Write this statement as a conditional probability using correct mathematical notation. This probability is called the sensitivity of the test. 4. If a student has not cheated, the probability of getting a negative test result is 0.90. Write this statement as a conditional probability using correct mathematical notation. This probability is called the specificity of the test. Based on your answers to questions 3 and 4: 5. If a student has cheated, what is the probability that the test will return a negative result? (That is, the test incorrectly concludes the student did not cheat.) This is called the false negative rate of the test. 6. If a student not cheated, what is the probability that the test will return a positive test result? (That is, the test incorrectly concludes that the student cheated.) This is called the false positive rate of the test. Calculating with probability Use the rules of conditional probability to answer the following questions. Show or explain your work for all calculations. (Hint: look at the example on page 235 of your text). 7. What is the probability that a randomlychosen student @ cheat and gets a positive result (the test correctly says that the student cheated)? 8. What is the probability that a randomly-chosen student did n_ot cheat and gets a negative result (the test correctly says that the student did not cheat)? 10 90% l:l- 20f3 10:38 AM Serum blood Diagnosis cholesterol Less than 180 Ideal for people with heart disease 180-200 Normal 200240 Borderline high 240 and above High A person is chosen at random from the population. Using StatCrunch software, answer the following questions. For all questions in Part B, express your answers using correct mathematical notation for probability, write that probability in a complete English sentence, and show the corresponding graph of the normal distribution. 1. What is the probability that the person's cholesterol is ideal? To do this calculation: i. Login to MyMathLab. Click on StatCrunch on the left side of the course homepage. ii. Click on \"datasets from your textbook\" in the middle of the screen. iii. Click on the Stat button at the top ofthe spreadsheet, then choose "Calculators" and then "Normal.\" This calculator will help you calculate probabilities based on the normal distribution. iv. Enter the mean and standard deviation of cholesterol for this population. v. Enter the value 180 on the next line, so that it reads "P(X3180)=\" then click Compute. vi. Click on Options in the upper left corner of the window, then select Copy and follow the instructions to copy the graph. Paste that picture into the Word document where you are preparing your report. 2. What is the probability that his cholesterol is high? To do this calculation: Follow the steps for question 1, but click on the s symbol (less than or equal) to change it to 2 (greater than or equal). What value does cholesterol need to be greater than or equal to? 10 90% l:l- Since person's cholesterol is ideal 1when x