PLEASE CLEARLY STATE WHICH ANSWER CHOICE IS CORRECT!!! A, B, C, or D.

then follow up with a short explanation of why that is the correct answer.

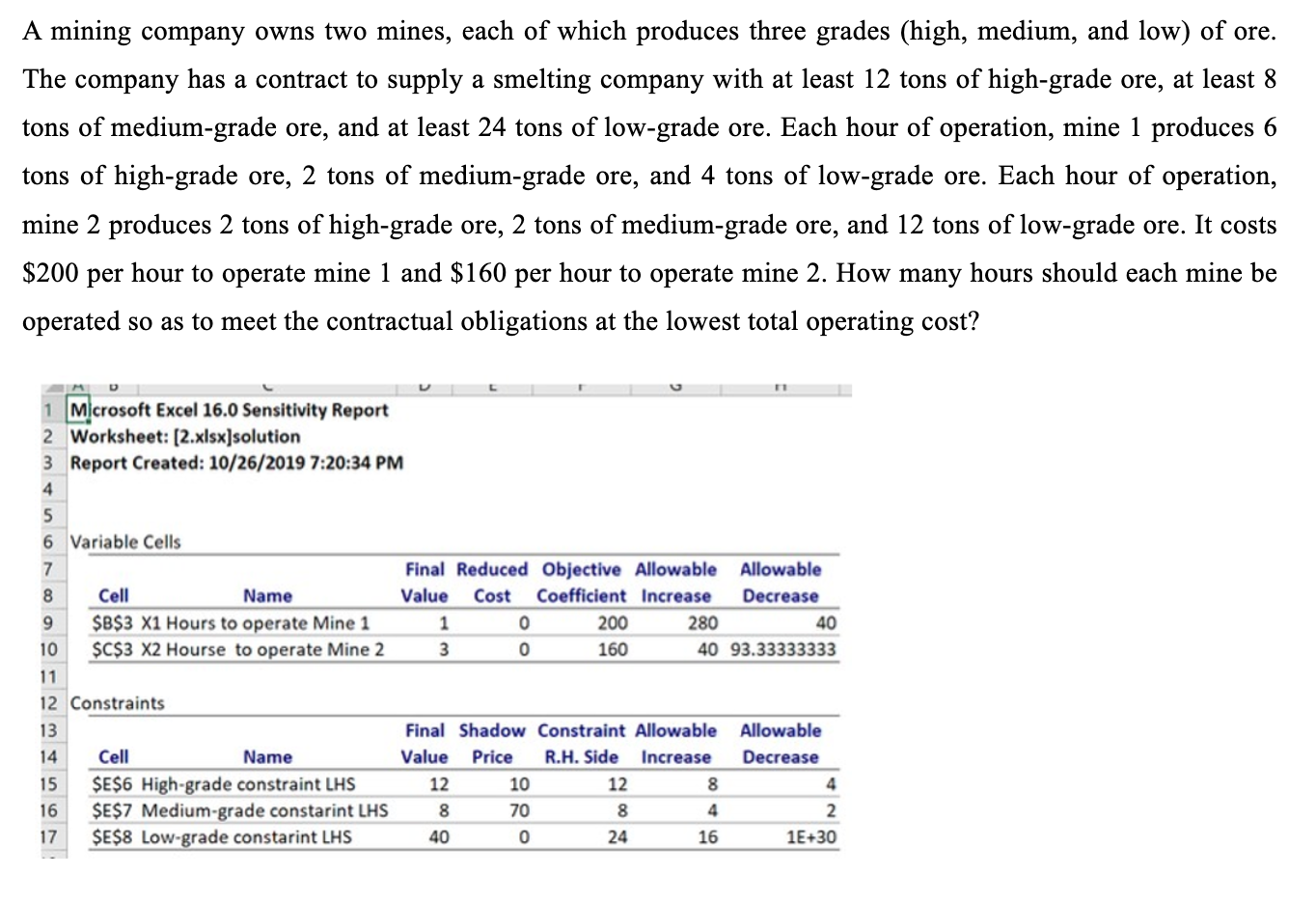
A mining company owns two mines, each of which produces three grades (high, medium, and low) of ore. The company has a contract to supply a smelting company with at least 12 tons of high-grade ore, at least 8 tons of medium-grade ore, and at least 24 tons of low-grade ore. Each hour of operation, mine 1 produces 6 tons of high-grade ore, 2 tons of medium-grade ore, and 4 tons of low-grade ore. Each hour of operation, mine 2 produces 2 tons of high-grade ore, 2 tons of medium-grade ore, and 12 tons of low-grade ore. It costs $200 per hour to operate mine 1 and $160 per hour to operate mine 2 . How many hours should each mine be operated so as to meet the contractual obligations at the lowest total operating cost? Use this sensitivity report to answer the questions below. If the high-grade ore requirement was raised to 15 tons: What minimum Cost could be realized? Would the optimal solution change? Increasing the RHS of the high-grade ore constraint by 3 is within the allowable increase of 16 so the shadow price of $0 is operative (i.e., each 1-ton increase in the RHS adds nothing to the current minimum cost). Thus, the minimum Cost would be the same $680 and the optimal solution will not change. Increasing the RHS of the high-grade ore constraint by 3 is within the allowable increase of 4 so the shadow price of $70 is operative (i.e., each 1-ton increase in the RHS adds $70 to the current minimum cost). Thus, the minimum Cost would be $680+3($70)=$890. Yes, the optimal solution will change (because a more costly- $890 versus $680--mine operation plan would be necessary to obtain more high-grade ore). Increasing the RHS of the high-grade ore constraint by 3 is within the allowable increase of 8 so the shadow price of $10 is operative (i.e., each 1-ton increase in the RHS adds $10 to the current minimum cost). Thus, the minimum Cost would be $680+3($10)=$710. Yes, the optimal solution will change (because a more costly-- $710 versus $680--mine operation plan would be necessary to obtain more high-grade ore). None of the above