Please help and explain. Determine the value of the equilibrium constant (K) using the t= infinity equilibrium at 29.1oC and graph on the excel. 
 Given Data:
Given Data: 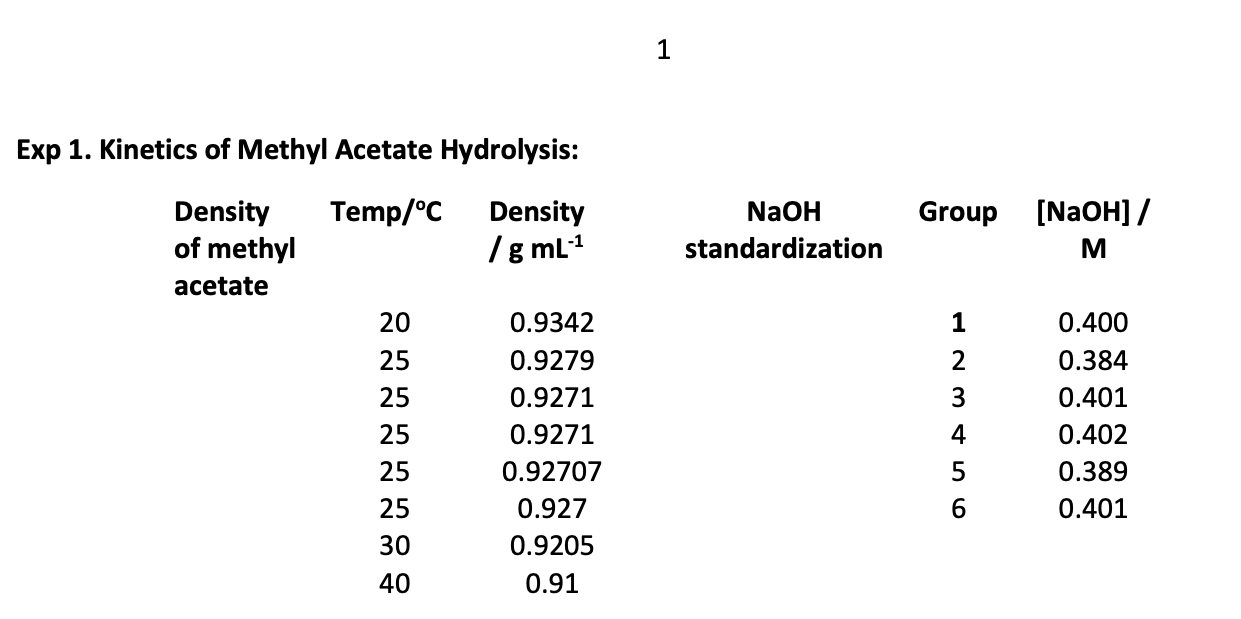
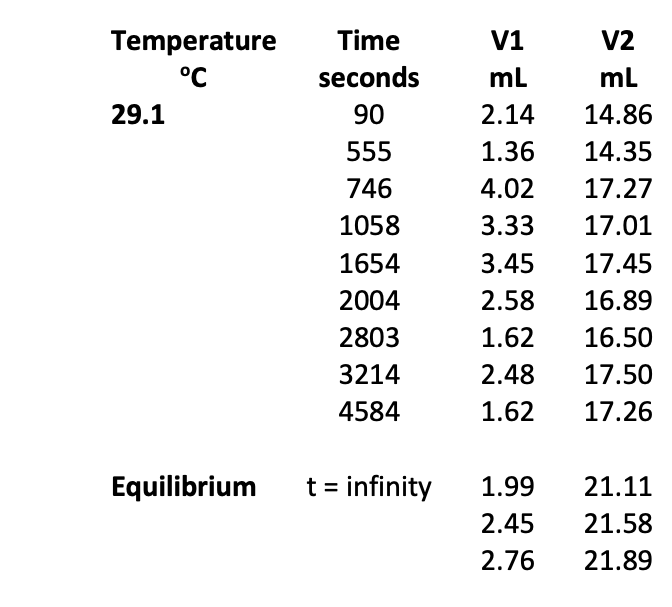
To calculate the infinite time titration, we have to proceed as follows: Initial moles of methyl acetate = (5.00 ml x density / Molar Mass) (26) = (5.00 ml x 0.9273 g ml*'/ 74.08g mol-4) (at 25C) = 6.259 x 10-2 mol This would have been the moles of acetic acid produced if the reaction has gone to completion instead of equilibrium. In a 5.00 ml aliquot of the reaction solution, the number of moles of acetic acid produced, had the reaction gone to completion, would be: 6.259 x 10-2 mols x (5.0 mL / 104.6 mL) = 2.99 10-3 mols (27) 100 mL of 1.0 M HCl or 0.1 moles of HCl was added to the reaction flask. The 104.6 mL comes from the 100 mL of HCl and the 5.0 mL of methyl acetate. Can you give a reason why the volumes of these two liquids is not additive when mixed? The number of moles of hydrochloric acid in a 5.0 ml aliquot is therefore: 0.1 x (5.00 mL / 104.6 mL) = 0.00478 mol (28) The maximum moles of acid possible in the 5.0 ml aliquot of reaction mixture is therefore the sum of the hydrochloric and the acetic acids: 0.00478 +2.99 x 10-3 = 7.77 x 10-3 total moles of acid (29) The volume of NaOH solution (V.) needed if the reaction did go to completion would be: 7.77 7.77 x 103 V = -X1000 = (30) M NaOH MNOH But the reaction doesn't go to completion; it reaches equilibrium so we must account for this difference. Let Vt be the volume of 0.4M NaOH solution (in milliliters) required to neutralize the 5.00 mL aliquots withdrawn at various times, t. Provided the volume of the solution does not change, Vt is the volume of NaOH that neutralizes the constant moles of HCl in the aliquot plus the variable amount of acetic acid due to the hydrolysis of the methyl acetate. The difference Voo-Vt is simply a measure of unreacted methyl acetate still in the aliquot at time t. (V. - Vt) MNaOH is the moles of methyl acetate remaining in the aliquot. M [CH,COOCH3] 1 naoh (V. - V.) = (31) 5.0 Thus (VOC-Vt) is a measure of the concentration of methyl acetate in the reaction mixture as a function of time. Thus, provided the reverse reaction in the reaction mixture is neglected, a graph of In(V20-Vt) versus time should be linear with a slope equal to the rate constant. Check to see if the graph deviates from linearity as the reaction proceeds and more and more products are formed. Determine the extent of the reaction at which any non-linearity in the graph is observed. Neglecting the reverse reaction is only valid when the concentrations of acetic acid and methanol are small and this will only be true when most of the methyl acetate has not reacted. You can also calculate the concentration of all the species at several times during your kinetic run to see what the concentrations of methanol and acetic acid are. In order to determine the value of the equilibrium constant we can use the value of Vt, when the reaction has reached equilibrium. M NaOH (V. - VC) [CH,COOCH, Jeg (32) 5.0 and zeg [CH,COOH].q =[CH3OH].q Mnaoh (V, 9-v.) (33) 5.0 where Vo is the titration of the 5.0 mL aliquot at time t= 0. From these data we can calculate the equilibrium constant: [CH,COOH)eq[CH,OH)eq K. = (34) [CH,COOCH3 Jeg Report your calculated equilibrium constant (and its error) at your bath temperature to the instructor. When the entire class has reported their equilibrium constant values (with error!) to the instructor, you will then plot the natural log of these equilibrium constants versus 1/T (where T is temperature in Kelvin). The slope of the resulting plot will be related to the enthalpy and the intercept related to the entropy (see Erying theory). You will perform regression analysis on this plot to determine the error in both of these values. Also include in your report AG for the reaction with error. Once you have determined the equilibrium constant and the rate constant for the forward reaction, we can use the following relation to determine the rate constant for the reverse reaction (35) k[CH,COOCH3 leq = k [CH,COOH)eq[CH,OH]e, k [CH,COOCH3 Jeg k = [CH,COOH)eq[CH,OH]e, Using an Excel spreadsheet table like the one below to record your data and calculate your results. (36) 1 Exp 1. Kinetics of Methyl Acetate Hydrolysis: Temp/C Density of methyl acetate Density Ig mL-1 NaOH standardization Group (NaOH] / M 1 2 3 20 25 25 25 25 25 30 0.9342 0.9279 0.9271 0.9271 0.92707 0.927 0.9205 0.91 Imtin 0.400 0.384 0.401 0.402 0.389 0.401 4 5 6 40 Temperature C 29.1 Time seconds 90 555 746 1058 1654 2004 2803 3214 4584 V1 mL 2.14 1.36 4.02 3.33 3.45 2.58 1.62 2.48 1.62 V2 mL 14.86 14.35 17.27 17.01 17.45 16.89 16.50 17.50 17.26 Equilibrium t = infinity 1.99 2.45 2.76 21.11 21.58 21.89 To calculate the infinite time titration, we have to proceed as follows: Initial moles of methyl acetate = (5.00 ml x density / Molar Mass) (26) = (5.00 ml x 0.9273 g ml*'/ 74.08g mol-4) (at 25C) = 6.259 x 10-2 mol This would have been the moles of acetic acid produced if the reaction has gone to completion instead of equilibrium. In a 5.00 ml aliquot of the reaction solution, the number of moles of acetic acid produced, had the reaction gone to completion, would be: 6.259 x 10-2 mols x (5.0 mL / 104.6 mL) = 2.99 10-3 mols (27) 100 mL of 1.0 M HCl or 0.1 moles of HCl was added to the reaction flask. The 104.6 mL comes from the 100 mL of HCl and the 5.0 mL of methyl acetate. Can you give a reason why the volumes of these two liquids is not additive when mixed? The number of moles of hydrochloric acid in a 5.0 ml aliquot is therefore: 0.1 x (5.00 mL / 104.6 mL) = 0.00478 mol (28) The maximum moles of acid possible in the 5.0 ml aliquot of reaction mixture is therefore the sum of the hydrochloric and the acetic acids: 0.00478 +2.99 x 10-3 = 7.77 x 10-3 total moles of acid (29) The volume of NaOH solution (V.) needed if the reaction did go to completion would be: 7.77 7.77 x 103 V = -X1000 = (30) M NaOH MNOH But the reaction doesn't go to completion; it reaches equilibrium so we must account for this difference. Let Vt be the volume of 0.4M NaOH solution (in milliliters) required to neutralize the 5.00 mL aliquots withdrawn at various times, t. Provided the volume of the solution does not change, Vt is the volume of NaOH that neutralizes the constant moles of HCl in the aliquot plus the variable amount of acetic acid due to the hydrolysis of the methyl acetate. The difference Voo-Vt is simply a measure of unreacted methyl acetate still in the aliquot at time t. (V. - Vt) MNaOH is the moles of methyl acetate remaining in the aliquot. M [CH,COOCH3] 1 naoh (V. - V.) = (31) 5.0 Thus (VOC-Vt) is a measure of the concentration of methyl acetate in the reaction mixture as a function of time. Thus, provided the reverse reaction in the reaction mixture is neglected, a graph of In(V20-Vt) versus time should be linear with a slope equal to the rate constant. Check to see if the graph deviates from linearity as the reaction proceeds and more and more products are formed. Determine the extent of the reaction at which any non-linearity in the graph is observed. Neglecting the reverse reaction is only valid when the concentrations of acetic acid and methanol are small and this will only be true when most of the methyl acetate has not reacted. You can also calculate the concentration of all the species at several times during your kinetic run to see what the concentrations of methanol and acetic acid are. In order to determine the value of the equilibrium constant we can use the value of Vt, when the reaction has reached equilibrium. M NaOH (V. - VC) [CH,COOCH, Jeg (32) 5.0 and zeg [CH,COOH].q =[CH3OH].q Mnaoh (V, 9-v.) (33) 5.0 where Vo is the titration of the 5.0 mL aliquot at time t= 0. From these data we can calculate the equilibrium constant: [CH,COOH)eq[CH,OH)eq K. = (34) [CH,COOCH3 Jeg Report your calculated equilibrium constant (and its error) at your bath temperature to the instructor. When the entire class has reported their equilibrium constant values (with error!) to the instructor, you will then plot the natural log of these equilibrium constants versus 1/T (where T is temperature in Kelvin). The slope of the resulting plot will be related to the enthalpy and the intercept related to the entropy (see Erying theory). You will perform regression analysis on this plot to determine the error in both of these values. Also include in your report AG for the reaction with error. Once you have determined the equilibrium constant and the rate constant for the forward reaction, we can use the following relation to determine the rate constant for the reverse reaction (35) k[CH,COOCH3 leq = k [CH,COOH)eq[CH,OH]e, k [CH,COOCH3 Jeg k = [CH,COOH)eq[CH,OH]e, Using an Excel spreadsheet table like the one below to record your data and calculate your results. (36) 1 Exp 1. Kinetics of Methyl Acetate Hydrolysis: Temp/C Density of methyl acetate Density Ig mL-1 NaOH standardization Group (NaOH] / M 1 2 3 20 25 25 25 25 25 30 0.9342 0.9279 0.9271 0.9271 0.92707 0.927 0.9205 0.91 Imtin 0.400 0.384 0.401 0.402 0.389 0.401 4 5 6 40 Temperature C 29.1 Time seconds 90 555 746 1058 1654 2004 2803 3214 4584 V1 mL 2.14 1.36 4.02 3.33 3.45 2.58 1.62 2.48 1.62 V2 mL 14.86 14.35 17.27 17.01 17.45 16.89 16.50 17.50 17.26 Equilibrium t = infinity 1.99 2.45 2.76 21.11 21.58 21.89

 Given Data:
Given Data: 







