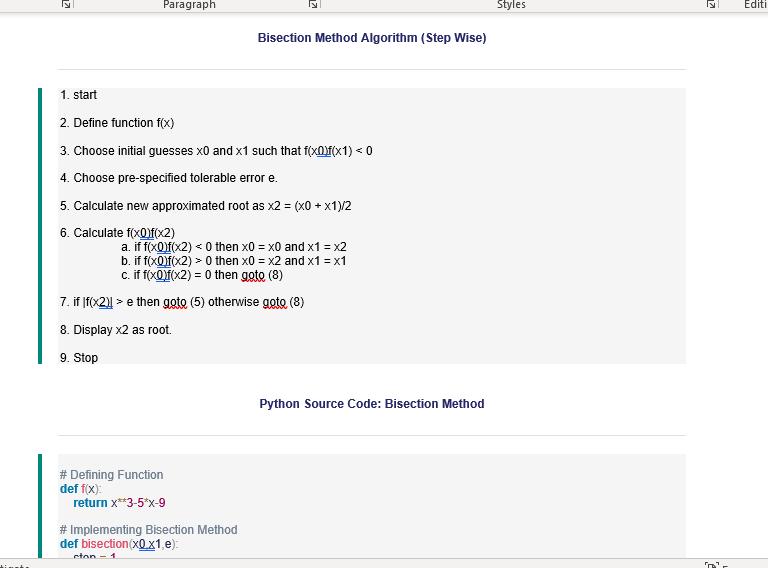
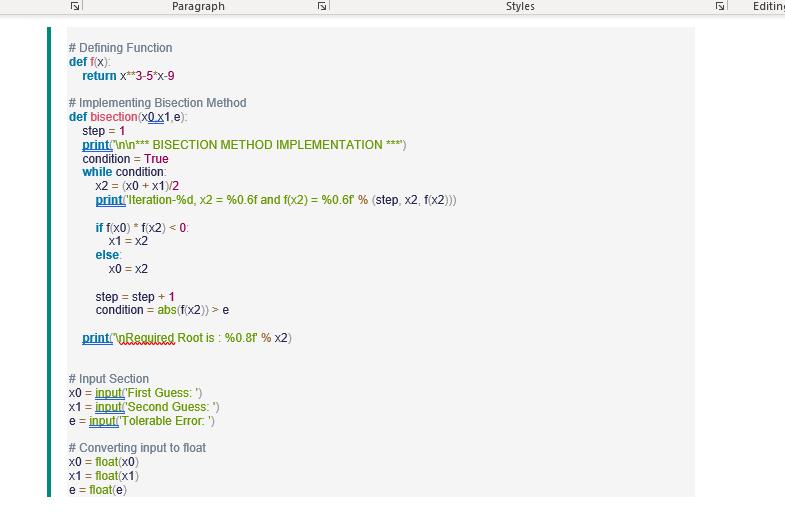
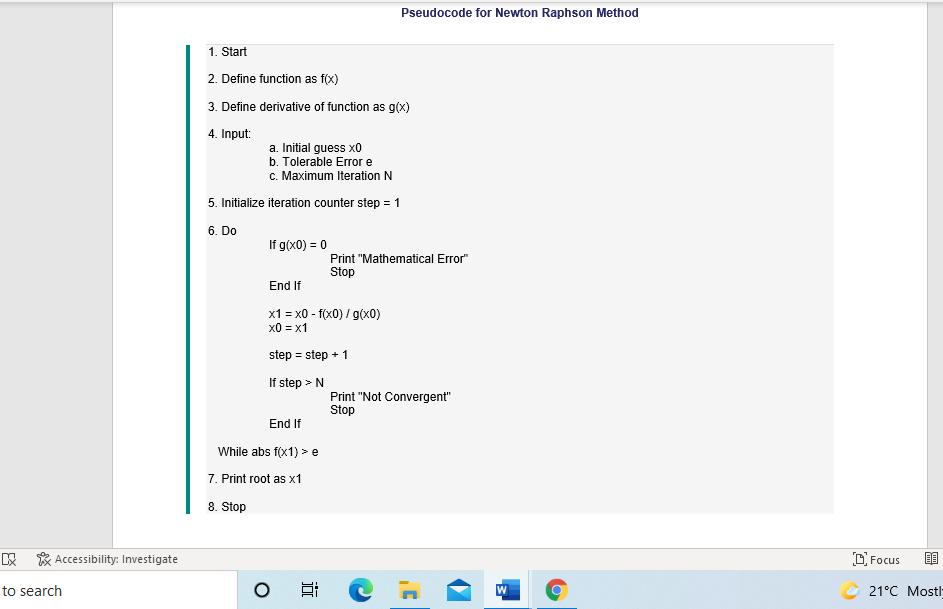
There are several methods to determine the roots of a polynomial numerically. Two of the most popular methods is the Newton-Raphson Method and the Bisection Method. Below is the Pseudo code as well as the Python program to determine the roots using these two methods. You need to understand how these two methods work. For the assignment, you are required to do the following: 1) Discuss the mathematics underpinning these two methods. 2) Using the PYTHON program given, draw up the flow diagram. 3) Do not copy the pseudocode given but redo the pseudocode in your own words. 4) Write down the PYTHON program given. Newton-Raphson Method: Pseudocode for Newton Raphson Method 1. Start 2. Define function as f(x) 3. Define derivative of function as g(x) Pseudocode for Newton Raphson Method 1. Start 2. Define function as f(x) 3. Define derivative of function as g(x) 4. Input: a. Initial guess x0 b. Tolerable Error e c. Maximum Iteration N 5. Initialize iteration counter step = 1 6. Do If g(x0) = 0 Print "Mathematical Error" Stop End If x1 = x0 - f(x0) / g(x0) x0 = x1 step = step + 1 If step > N Print "Not Convergent" Stop End If While abs f(x1) > e 7. Print root as x1 8. Stop E * Accessibility: Investigate D Focus to search 21C Mostl Python Source Code: Newton Raphson Method Function whose root is to be determined: f(x) = x - 5x -9 # Defining Function def f(x): return x*3 - 5x -9 # Defining derivative of function def g(x): return 3*x**2 - 5 # Implementing Newton Raphson Method def newtenRachson x0 e N) print inn*** NEWTON RAPHSON METHOD IMPLEMENTATION ****) step = 1 flag = 1 condition = True while condition: if g(x0) == 0.0 print 'Divide by zero error!") break x1 = x0 - f(x0/g(x0) print'Iteration-%d, x1 = %0.6f and f(x1) = %0.6f % (step, x1, f(x1)) x0 = x1 step = step + 1 if step > N: flag = 0 break condition = abs(fx1)) > e Paragraph Styles Editing flag = 0 break condition = abs(fx1)) > e if flag==1: print"nReauired root is: %0.8f % x1) else print aNat Convergent') # Input Section x0 = input('Enter Guess: ) e = input"Tolerable Error: ") N= input('Maximum Step: ') # Converting x0 and e to float x0 = float(x0) e = float(e) # Converting N to integer N = int(N) Paragraph Styles Editi Bisection Method Algorithm (Step Wise) 1. start 2. Define function f(x) 3. Choose initial guesses x0 and x1 such that f(x0)f(x1) < 0 4. Choose pre-specified tolerable error e. 5. Calculate new approximated root as x2 = (x0 + x1)/2 6. Calculate f(xOlf(x2) a. if f(x0)f(x2) < 0 then x0 = x0 and x1 = x2 b. if f(x0)f(x2) > 0 then x0 = x2 and x1 = x1 c.if f(x0)f(x2) = 0 then goto (8) !! 7. if If(x2)] > e then goto (5) otherwise goto (8) 8. Display x2 as root. 9. Stop Python Source Code: Bisection Method # Defining Function def f(x) return x**3-5*x-9 # Implementing Bisection Method def bisection(x0 x1,e): cton - 1 12 Paragraph Styles Editing # Defining Function def f(x): return x**3-5*x-9 # implementing Bisection Method def bisection(x0 x1.e). step = 1 print in** BISECTION METHOD IMPLEMENTATION ***) condition = True while condition: x2 = (x0 + x1)/2 print Iteration-%d, x2 = %0.6f and f(x2) = %0.6f % (step, x2, f(x2)) if fx0) * f(x2) < 0: x1 = x2 else: x0 = x2 step = step + 1 condition = abs(fx2)) > e printaReauiced Root is : %0.8f % x2) # Input Section x0 = input"First Guess: ') x1 = inputt Second Guess: ") e = input("Tolerable Error. ") # Converting input to float x0 = float(x0) x1 = float(x1) e = float(e) Pseudocode for Newton Raphson Method 1. Start 2. Define function as f(x) 3. Define derivative of function as g(x) 4. Input: a. Initial guess x0 b. Tolerable Error e c. Maximum Iteration N 5. Initialize iteration counter step = 1 6. Do If g(x0) = 0 Print "Mathematical Error" Stop End If x1 = x0 - f(x0) / g(x0) x0 = x1 step = step + 1 If step > N Print "Not Convergent" Stop End If While abs f(x1) > e 7. Print root as x1 8. Stop E * Accessibility: Investigate D Focus to search 21C Mostl