Please help. I've tried writing the code but am getting nowhere. I don't understand how to write the loop.

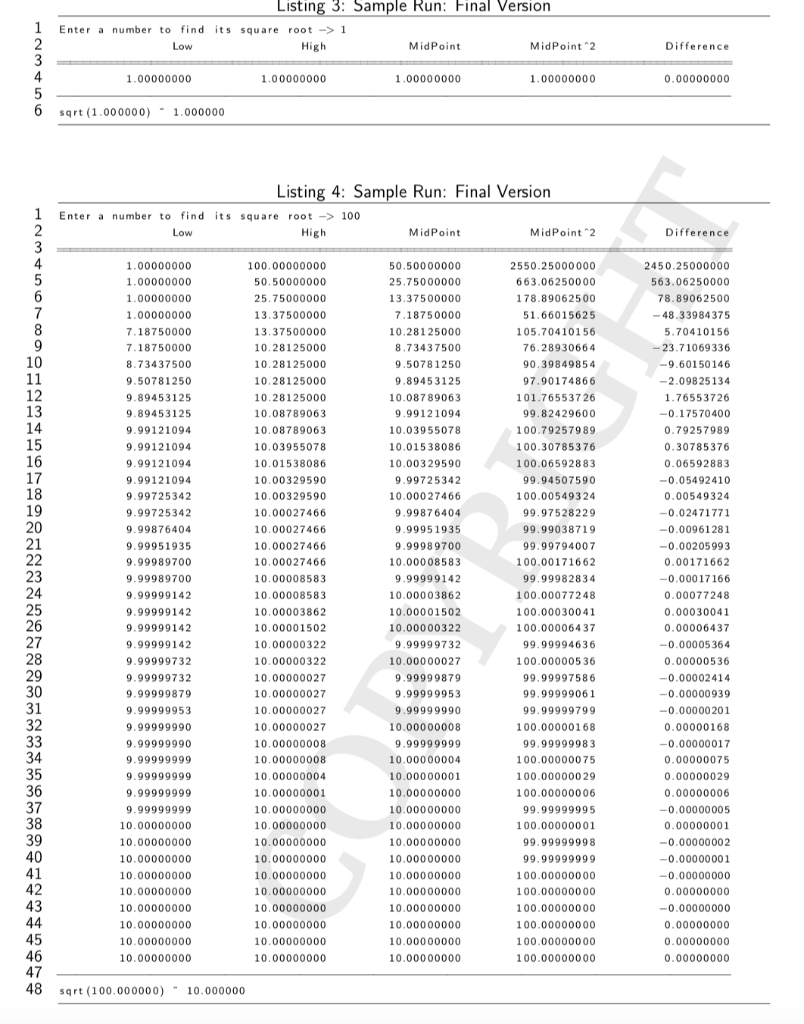
Finding the Square Root of a Number Out: 2/12 Due: 2/25 by 11:50 PM Using a Loop Formatting Output Simulating an Iterative Process In this project, you will write an interactive program, SquareRootFinder, that computes the square root of a number to the nearest ten billionths place, that is, 10 decimal digits Definition 1. The square root of a number n, denoted Vn, is a number s whose square is equal to n; that is, if the s is the square root of n There is an elementary algorithm used to find the square root of a number that takes advantage of a mathematical principle commonly referred to as the pinching (a.k.a. squeezing or sandwich) theorem. The theorem simply means that given any closed continuous interval [a, b, there is a number p such that a S p b. We can easily show that such a number.p, exists. , the midpoint between a and b, satisfies the inequality How does this relate to our square root algorithm? The square root of any number lies in a continous interval between two numbers. We know that Vn is between 0 and 1 if n is less than 1 and between 1 and n if n is greater than or equal to 1. We would like to keep narrowing, "squeezing", the initial interval to obtain better and better approximations of Vn. We can terminate the algorithm when our approximation is within some predetermined tolerance () For example to find v100, we first consider the initial interval 1, 100]. We then square 50.5, the midpoint of the interval. 50.550.5 100, so we can obtain a better approximation by squeezing our interval to its lower haf, 1,50.5]. Next, we consider the midpoint of this interval 25.75 25.75 100, so again we consider the lower half of the interval, 11.25.75]. 13.375 13.375 i 100, so we narrow the interval to 1, 13.375], the lower half of the interval. 7.1875x7.1875 i 100, so, this time, we narrow the interval to its upper half since v100 is greater than 7.1875 but less than 13.375. We use the interval 17.1875, 13.375. 10.28125x 10.28125 100, so we narrow the interval to its lower half, 7.1875, 10.28125], etc. If we continue to halve the interval to one containing the Vn, we will eventually obtain a midpoint whose square gives us 100. Due to truncation and roundoff errors by computers, we pick a very small number, so that if the approximation is within that tolerance, we terminate the algorithm and return the midpoint as the 'best' approximation of the square root of 100. The smaller the tolerance, the better the approximation. Our tolerance must be a small positive number. Formally, here is a pseudocode description of the square root algorithm Listing 1: A Square Root Algorithm 1 if n is a negative number sqrtNAN 3 otherwise 4 if n is a non-negative number less than 1 low-0 high :-1 otherwise low-1 high :-n 10 endIf mid :- lowthigh Repean until mid2n 12 13 14 15 16 17 18 19 20 21 endIf if mid-n100 100.00000000 50.50000000 25.75000000 13.37500000 13.37500000 50.50000000 25.75000000 2550.25000000 2450.25000000 663.06250000 1.00000000 8.33984375 3.71069336 2.0982513 1.00000000 7.18750000 10 10.28125000 90.39849854 12 13 76553726 -0.17570400 .76553726 10.08789063 10.03955078 100.79257989 0.79257989 16 10.00329590 10.00329590 00.06592883 99.94507590 100.00549324 10.00027466 0.009612 0.00205 10.00027466 10.00027466 10.00027466 10.00008583 10.00008583 10.00003862 10.00001502 10.00000322 10.00000322 10.00000027 9.99989700 10.00008583 99.99794007 9.99989700 9.99989700 9.99999142 9.99999142 9.99999142 9.9999914 0.00017166 10.00003862 10.00001502 10.00000322 100.00077248 100.00030041 100.00006437 0.00030041 0.00006437 0.00005364 0.00000536 9.99999732 9.99999732 9.99999879 10.00000027 100.00000536 0.00000939 99.99999061 99.9999979 100.00000168 99.99999983 31 9.99999990 9.99999990 9.99999999 9.99999999 9.99999999 9.99999999 10.00000000 10.00000000 10.00000000 10.00000000 10.00000027 10.00000027 10.00000008 10.00000008 10.00000004 10.00000001 10.00000000 0.00000168 10.00000008 9.99999999 10.00000004 10.00000001 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 0.00000017 100.00000029 100.00000006 99.99999995 100.00000001 99.99999998 99.99999999 100.00000000 100.00000000 100.00000000 100.00000000 100.00000000 100.00000000 0.00000029 0.00000006 -0.00000005 0.00000001 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 -0.00000000 10.00000000 10.00000000 10.00000000 0.00000000 0.00000000 0.00000000 48 sqrt (100.00000o) 10.000000