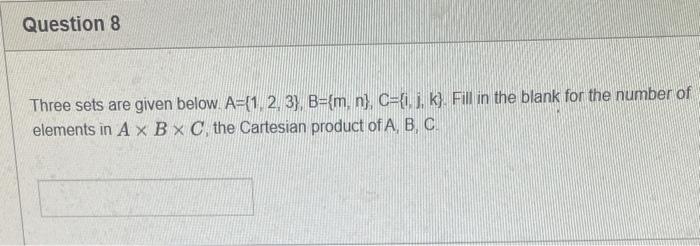
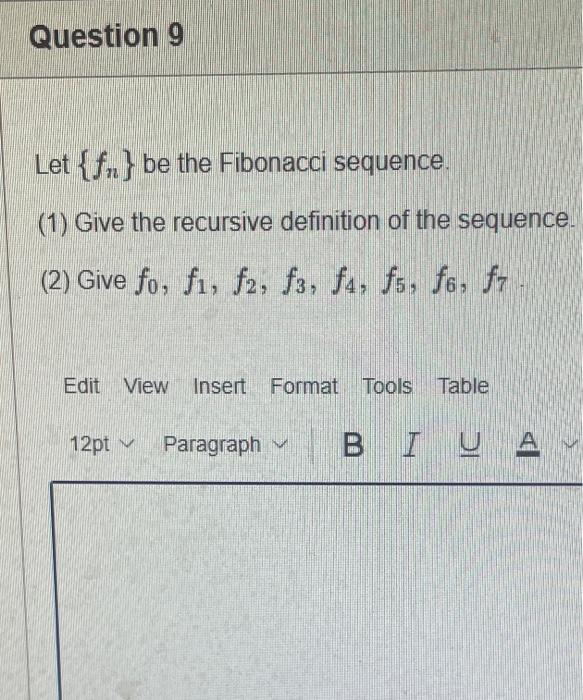
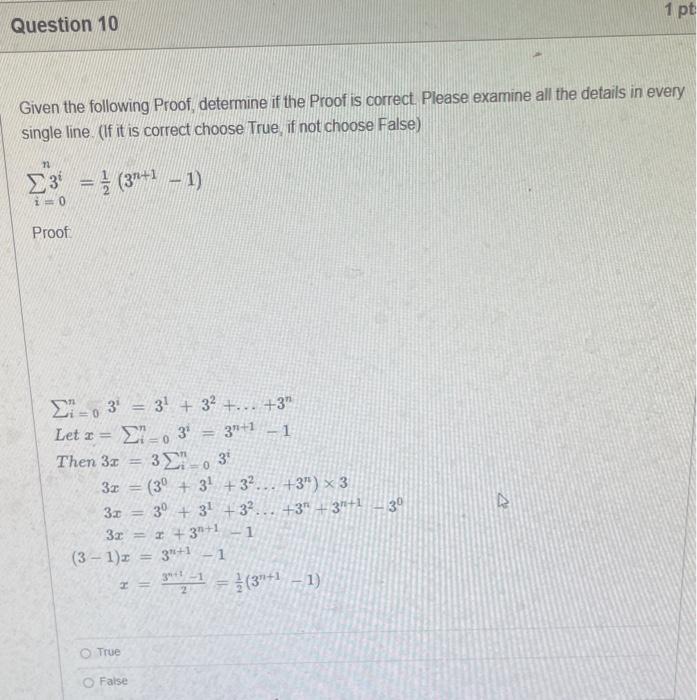
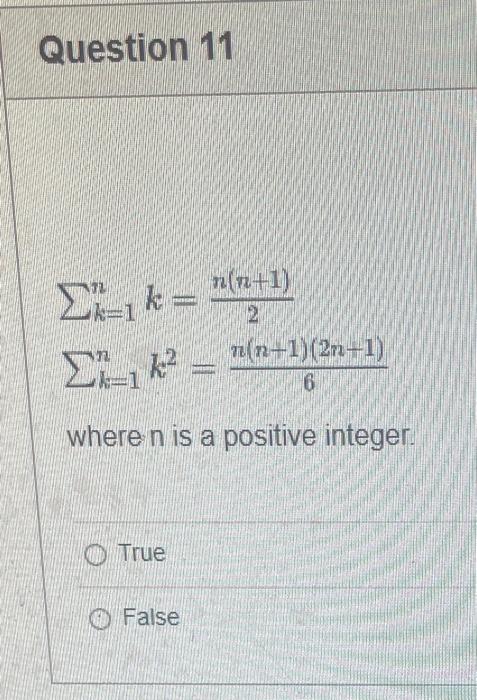
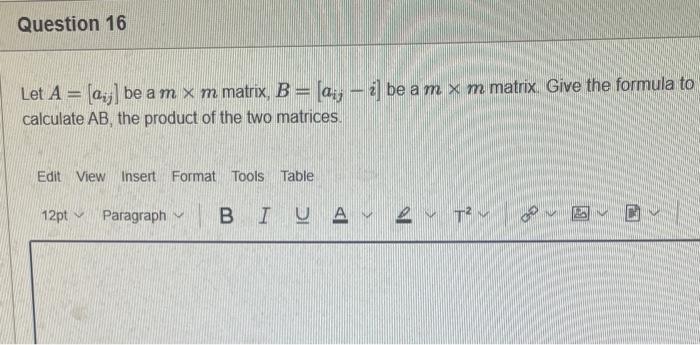
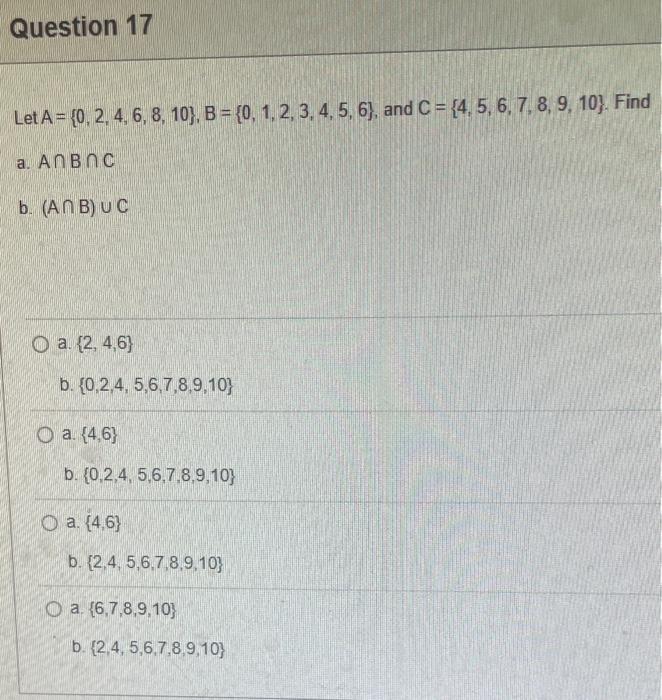
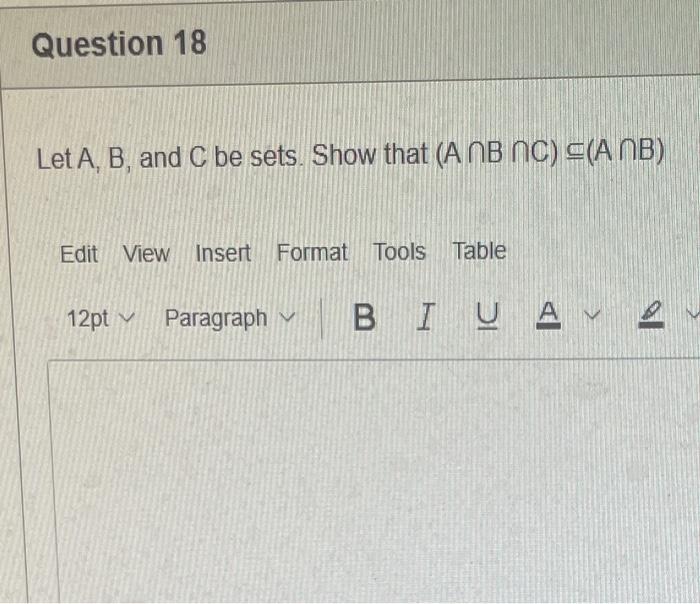
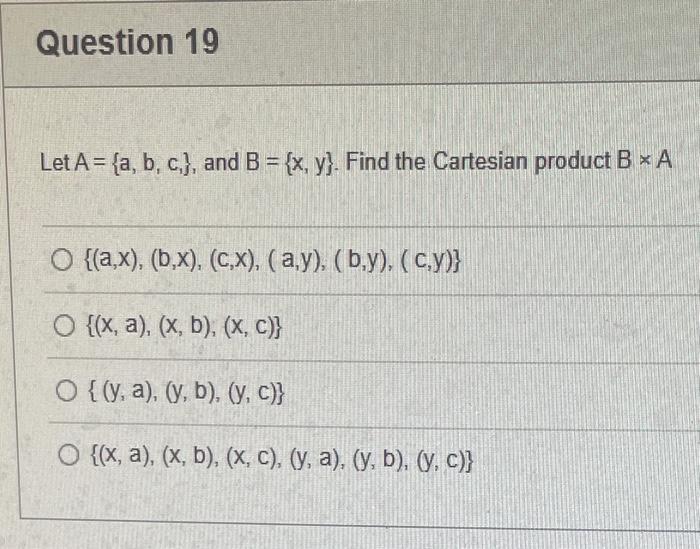
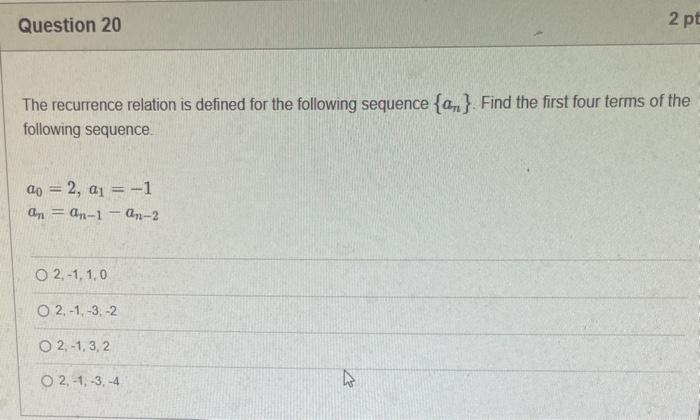
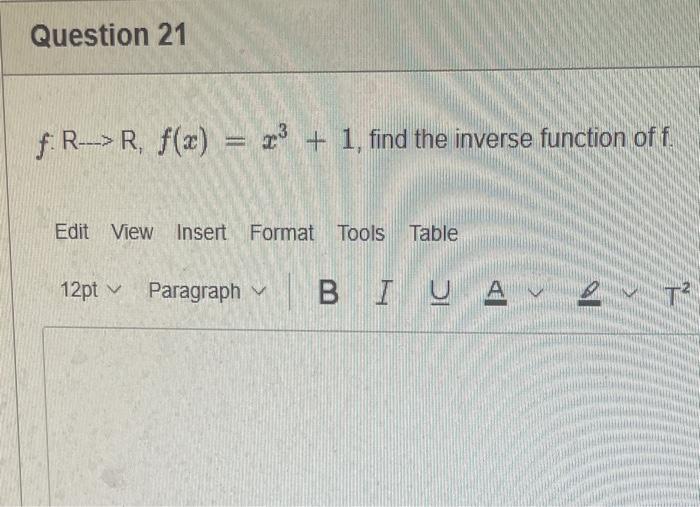
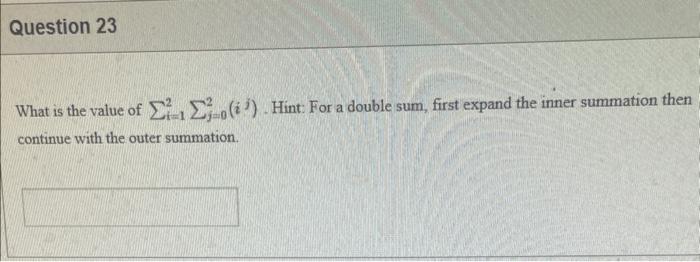
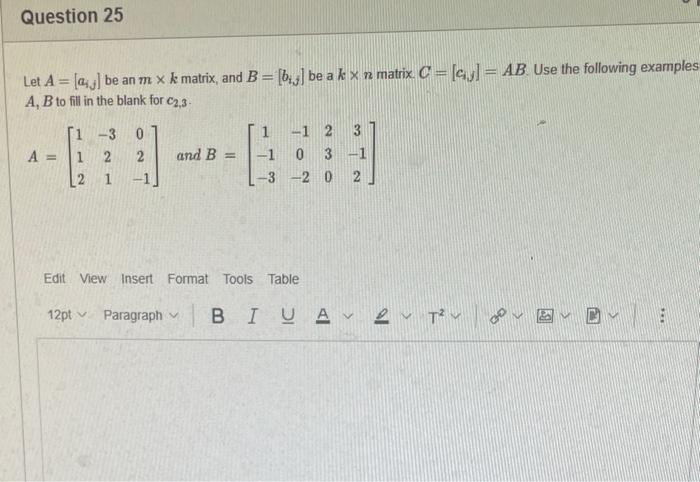
PLEASE HELP WITH ALL QUESTIONS THANK YOU!
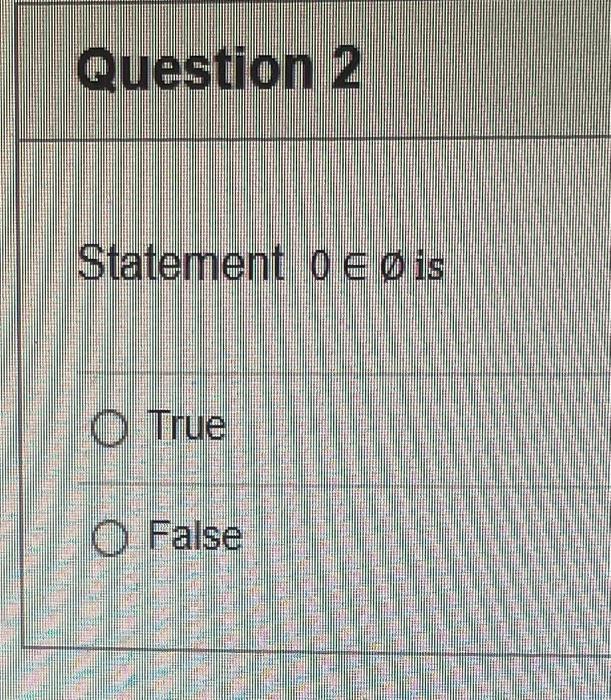
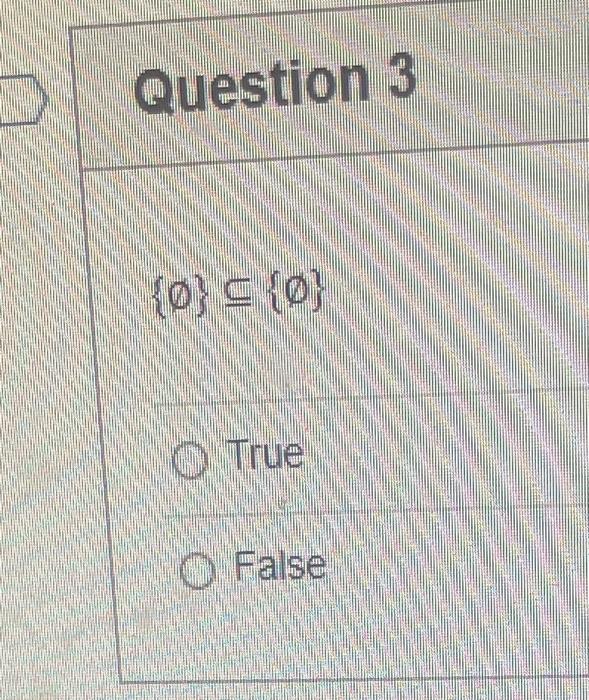
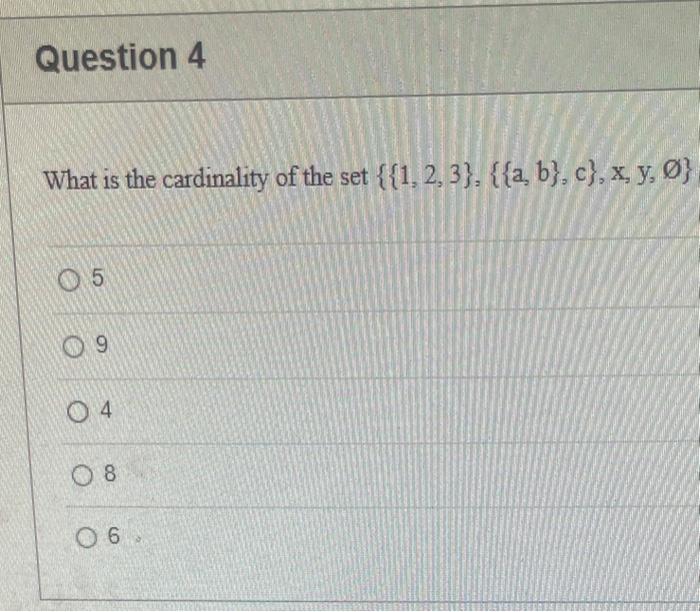
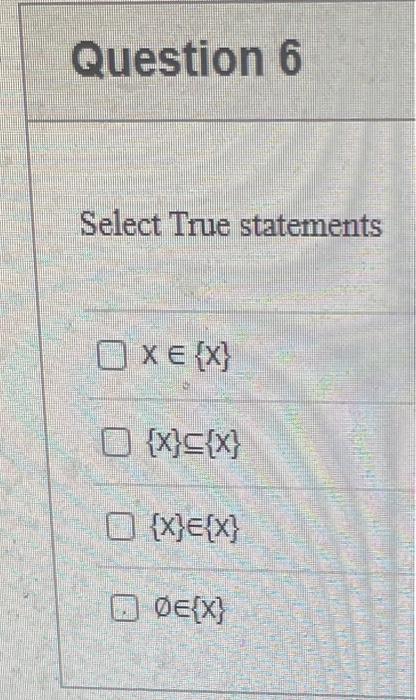
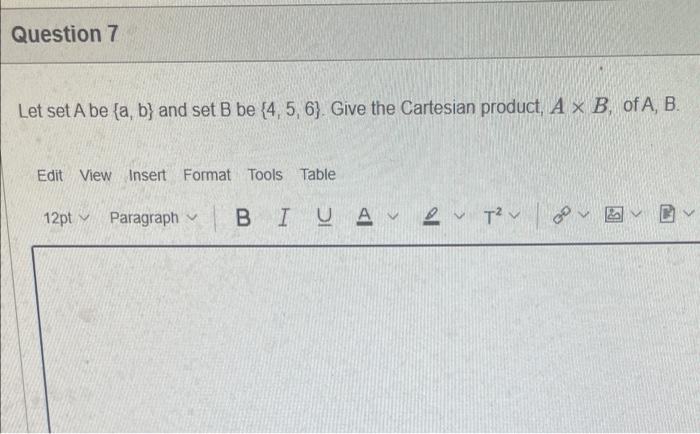
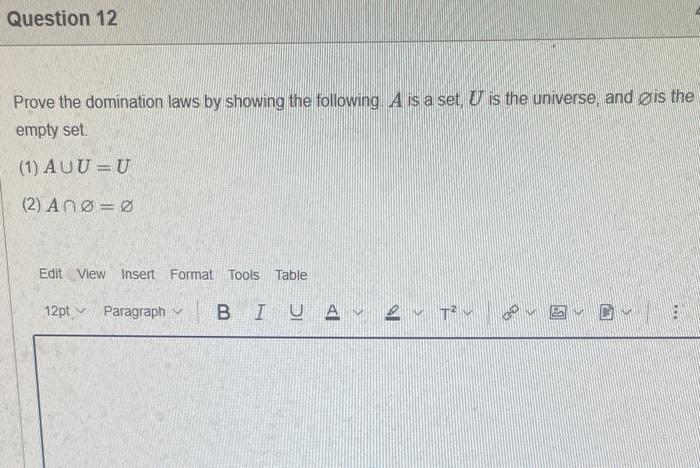
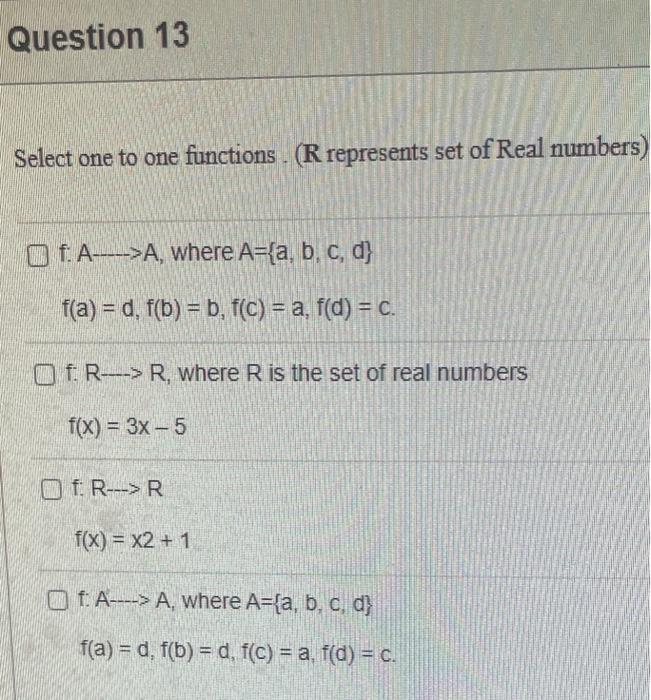
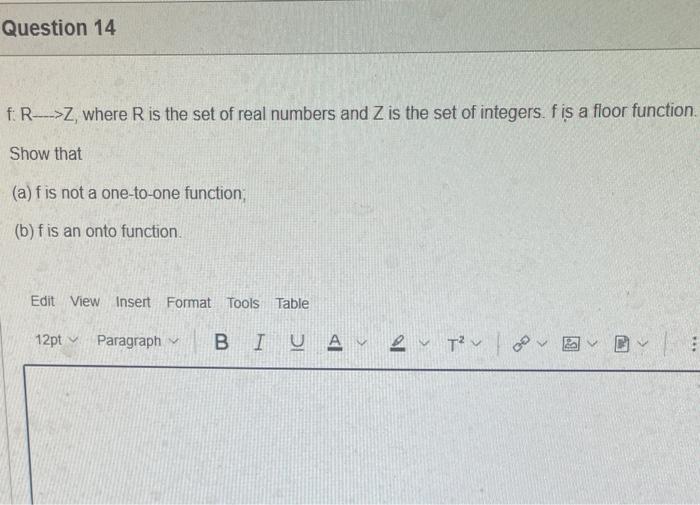
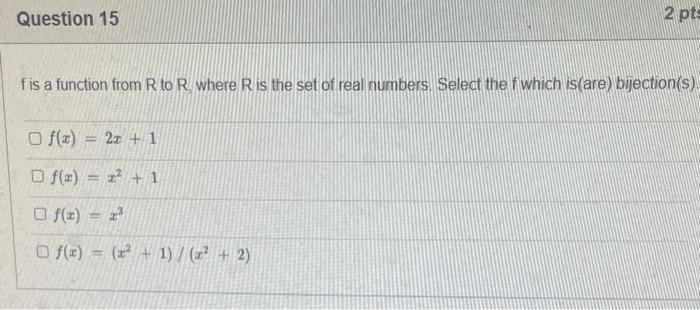
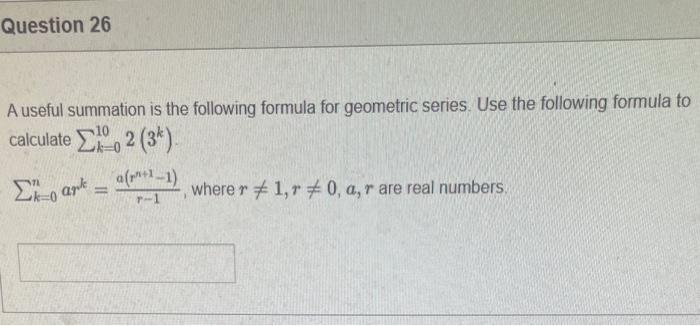
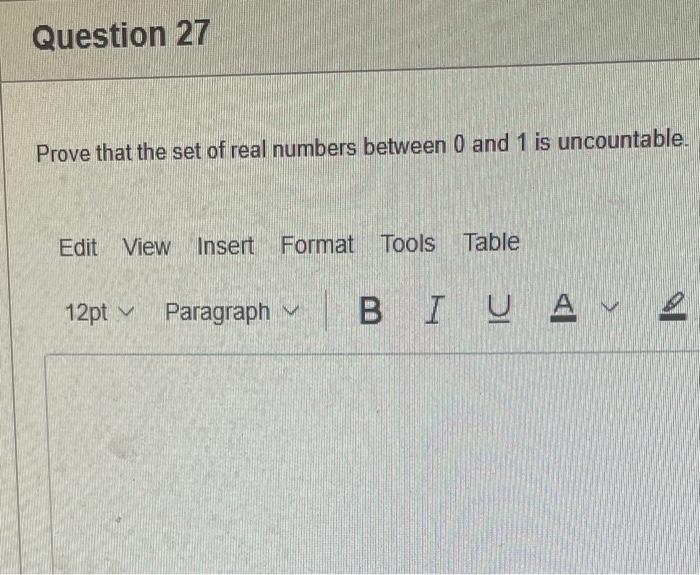
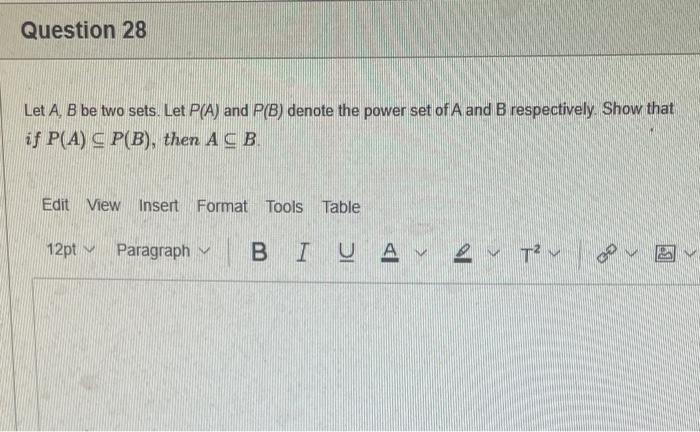
Statement 0 is True False {}{} True False What is the cardinality of the set {{1,2,3},{{a,b},c},x,y,} 5 9 4 8 6 Statement {0} is True False Select True statements x{x}{x}{x}{x}{x}{x} Let set A be {a,b} and set B be {4,5,6}. Give the Cartesian product, AB, of A,B. Three sets are given below. A={1,2,3},B={m,n},C={i,j,k}. Fill in the blank for the number of elements in ABC, the Cartesian product of A,B,C. Let {fn} be the Fibonacci sequence. (1) Give the recursive definition of the sequence. (2) Give f0,f1,f2,f3,f4,f5,f6,f7. Edit View Insert Format Tools Table 12pt Paragraph B=IBA Given the following Proof, determine if the Proof is correct. Please examine all the details in every single line. (If it is correct choose True, if not choose False) i=0n3i=21(3n+11) Proof: i=0n3i=31+32++3nLetx=i=0n3i=3n+11Then3x=3i=0n3i3x=(30+31+32+3n)33x=30+31+32+3n+3n+1303x=x+3n+11(31)x=3n+11x=23n+11=21(3n+11) True False k=1nk=2n(n+1)k=1nk2=6n(n+1)(2n+1) where n is a positive integer. True False Prove the domination laws by showing the following. A is a set, U is the universe, and is the empty set. (1) AU=U (2) A= Select one to one functions. (R represents set of Real numbers f. AA, where A={a,b,c,d} f(a)=d,f(b)=b,f(c)=a,f(d)=c. f:RR, where R is the set of real numbers f(x)=3x5 f. RR f(x)=x2+1 f:AA, where A={a,b,c,d} f(a)=d,f(b)=d,f(c)=a,f(d)=c f:RZ, where R is the set of real numbers and Z is the set of integers. f is a floor function. Show that (a) f is not a one-to-one function; (b) f is an onto function. f is a function from R to R, where R is the set of real numbers. Select the f which is(are) biection(s) f(x)=2x+1f(x)=x2+1f(x)=x3f(x)=(x2+1)/(x2+2) Let A=[aij] be a mm matrix, B=[aiji] be a mm matrix. Give the formula to calculate AB, the product of the two matrices. Question 17 Let A={0,2,4,6,8,10},B={0,1,2,3,4,5,6}, and C={4,5,6,7,8,9,10}. Find a. ABC b. (AB)C a. {2,4,6} b. {0,2,4,5,6,7,8,9,10} a. {4,6} b. {0,2,4,5,6,7,8,9,10} a. {4,6} b. {2,4,5,6,7,8,9,10} a. {6,7,8,9,10} b. {2,4,5,6,7,8,9,10} Let A,B, and C be sets. Show that (ABC)(AB) Let A={a,b,c,},andB={x,y}. Find the Cartesian product BA {(a,x),(b,x),(c,x),(a,y),(b,y),(c,y)} {(x,a),(x,b),(x,c)} {(y,a),(y,b),(y,c)} {(x,a),(x,b),(x,c),(y,a),(y,b),(y,c)} The recurrence relation is defined for the following sequence {an}. Find the first four terms of the following sequence. a0=2,a1=1an=an1an2 2,1,1,0 2,1,3,2 2,1,3,2 2,1,3,4 f:RR,f(x)=x3+1, find the inverse function of t. Suppose that a bank account initially has $1,000. This account yields 3% per year with interest compounded annually. Let Pn be the amount of money after n years. (a) Express Pn using a recurrence relation (or sometimes called recursive formula). (b) What is the ammount in the account after 20 years? What is the value of i=12j=02(ij). Hint For a double sum, first expand the inner summation then continue with the outer summation. j=08(2j+12j) 511 531 469 369 Let A=[ai,j] be an mk matrix, and B=[bi,j] be a kn matrix C=[cij]=AB. Use the following examples A,B to fill in the blank for C2,3. A=112321021andB=113102230312 A useful summation is the following formula for geometric series. Use the following formula to calculate k=0102(3k) k=0nark=r1a(rn+11), where r=1,r=0,a,r are real numbers. Prove that the set of real numbers between 0 and 1 is uncountable Let A,B be two sets. Let P(A) and P(B) denote the power set of A and B respectively. Show that if P(A)P(B), then AB