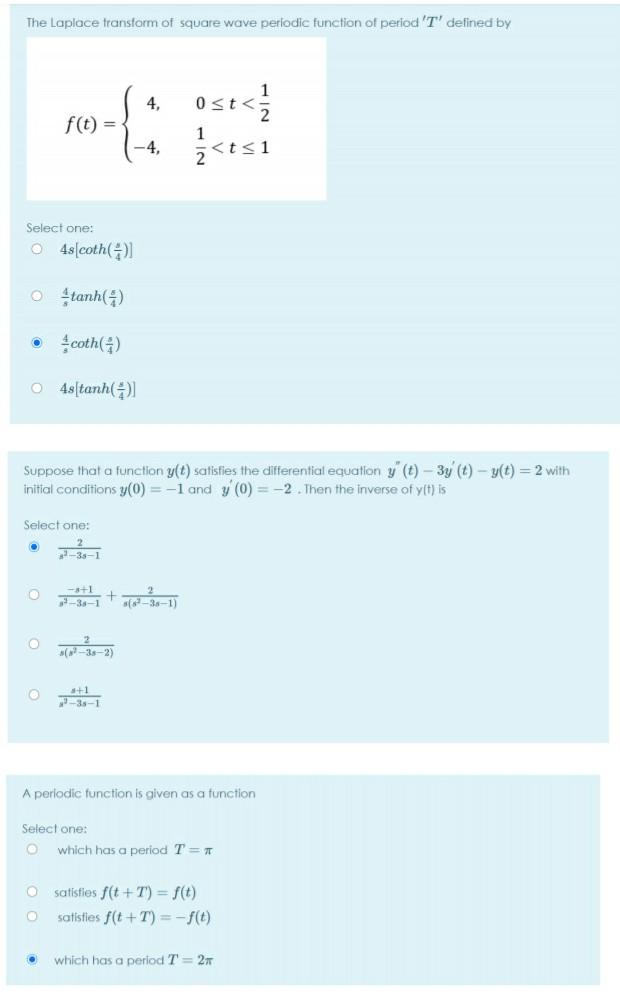
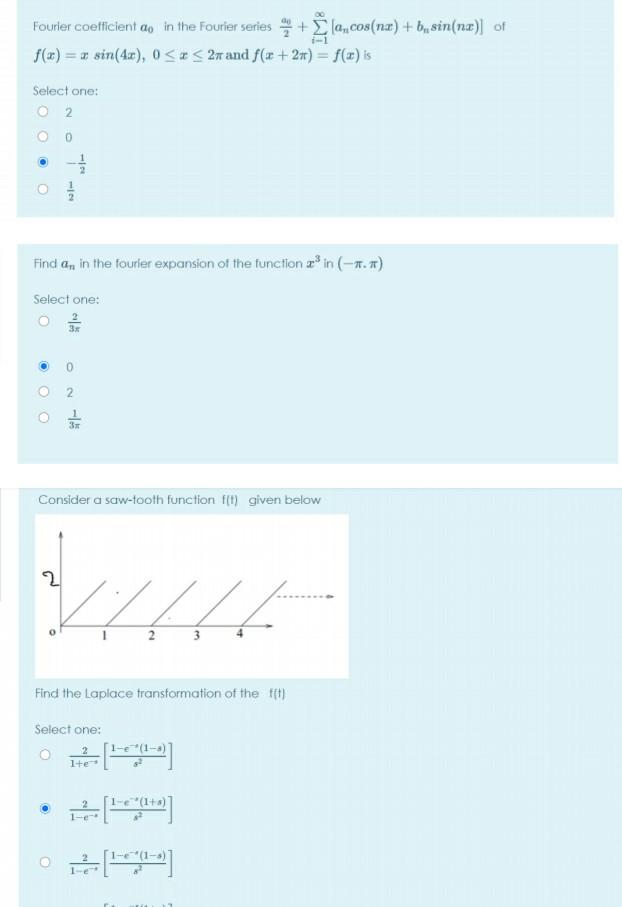
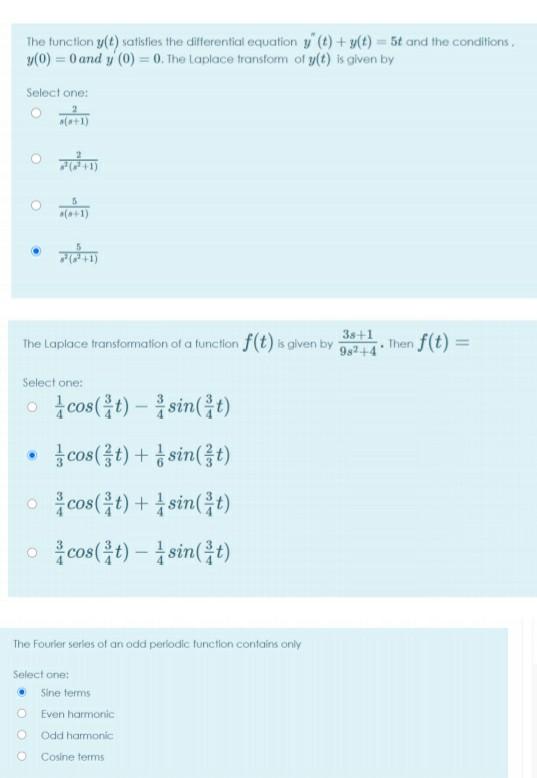
Which of the following is an odd function of t? Select one: t + sint Ot - 4t O cos(2t) + 6 In the Fourier series expansion of the function f(x) = x - 6 in (-1, 1), the value of bn = 0 Select one: True O False The function y(t) satisfies the differential equation y" (t) - 4y (t)- 5y(t) = 0 and the conditions, y(0) = 2 and y' (0) = 2. Then y(t) is given by Select one: e - -e-* o fest + let The Fourier constants for an odd function f(x) in the interval (-7, ) are given by. Select one: 2T ao = = f(x) dx, an=ff(x)cos(nx)dx, 2 bn=ff(x) sin(nx)dx, Obn=ff(x) sin(nx)dx, ao = an= O ao = f f(x) dx, an = f(x) cos(nx) dx, The inverse of the Laplace transformation of Select one: 01/2-1-1et f(x) dx, f(x) cos(nx)dx, 7/2 7/2 - -2t 1+e=2 + 1/2 + 1/{e= 1+1et -2t 1 8 (8+2) is The Laplace transform of square wave periodic function of period 'T' defined by Select one: 4s[coth()] O -tanh(-) coth() O 4stanh()] f(t) = Select one: O O Suppose that a function y(t) satisfies the differential equation y' (t) - 3y' (t)- y(t) = 2 with initial conditions y(0) = -1 and y' (0) = -2. Then the inverse of y(t) is O -38-1 -+1 -38-1 (-3-2) #+1 -35-1 1 4, 0st Fourier coefficient do in the Fourier series+la, cos(na) + b sin(nx)] of f(x) = sin(4x), 0x 2n and f(x + 2x) = f(x) is Select one: 02 12 Find an in the fourier expansion of the function in (-. ) Select one: ex Consider a saw-tooth function f(t) given below 2 WHE 2 3 Find the Laplace transformation of the f(t) Select one: 2 1+e 2 1-e 2 1-e [] [text] [] The Fourier constants for an odd function f(x) in the interval (-, ) are given by, Select one: O Obn=ff(x) sin(nx)dx, O ao=ff(x)da, af f(x)cos(na)da, ba=ff(r)sin(nx)da, O ao=ff(x)da, an = f(x)cos(nx)dx, The inverse of the Laplace transformation of ao=ff(x)dr, Select one: an= f(x)cos(nx)dx, 1-1-1et /N + 4 + e 0 14 + e Select one: O [2-1] [4n-8n] -2t -2t 1/2+1/et Find the Fourie coefficient b, where n 21 in the Fourier series expansion of f(x)=x-x in (0, 2T) $ (8+2) 4/ The function y(t) satisfies the differential equation y' (t) + y(t) = 5t and the conditions. y(0) = 0 and y' (0) = 0. The Laplace transform of y(t) is given by Select one: (1) a(+1) FOT The Laplace transformation of a function f(t) is given by Select one: cos(t) sin(t) cos(t) + sin(t) ocos (t) + sin(t) ocos (t) sin(t) The Fourier series of an odd periodic function contains only Select one: Sine terms O Even harmonic OOdd harmonic Cosine terms 38+1 98244 . Then f(t) =