Please provide a solution that does not exist on chegg because all of it are false and i voted downvote for all answers. Please provide the code without changing my code if you dont find any bugs and shortcoming. Please consider your code performs successfully for not only mentioned $2$matrix$.$ This is my method to use partial pivoting

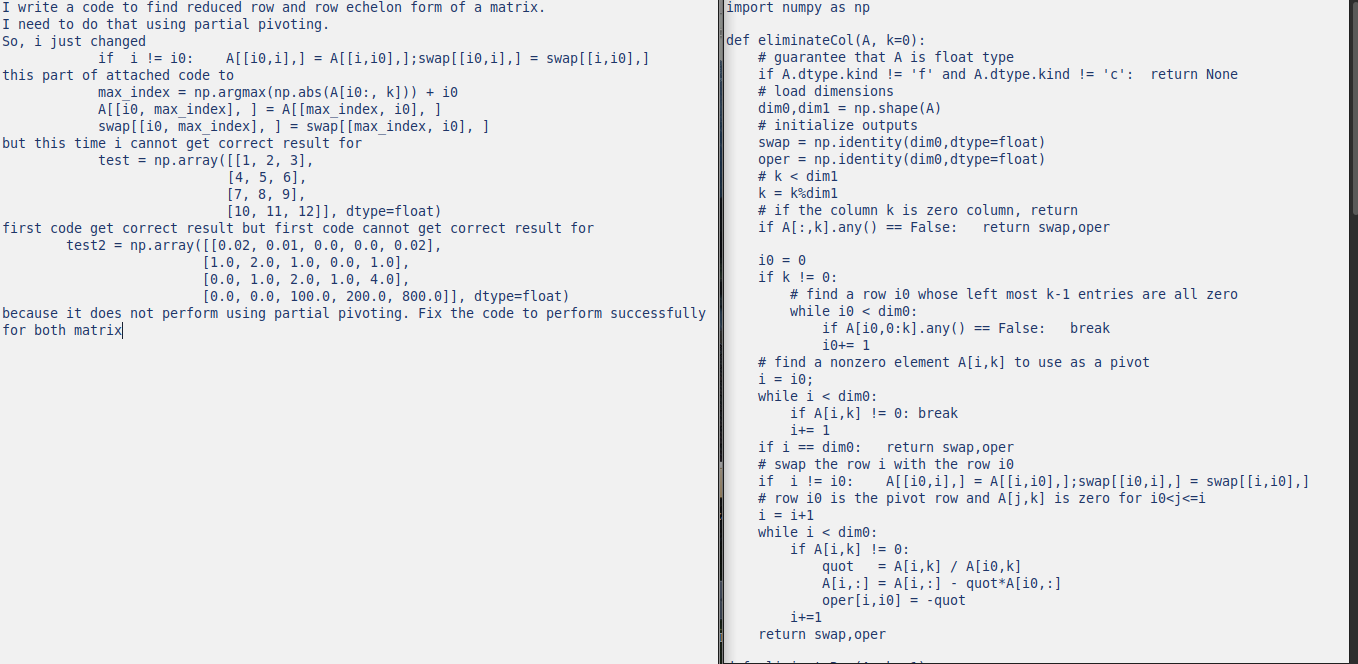
max$\_$index $=$np$.$argmax$($np$.$abs$($A$[$i$0$:$,$k$]))+$i$0$

$$ A$[[$i$0,$max$\_$index$],]=$A$[[$max$\_$index, i$0],]$; swap$[[$i$0,$max$\_$index$],]=$swap$[[$max$\_$index, i$0],]$

replace this code with

if i $!=$i$0$: A$[[$i$0,$i$],]=$A$[[$i$,$i$0],]$;swap$[[$i$0,$i$],]=$swap$[[$i$,$i$0],]$

then please read the problem in the attached image. Please dont provide complicated and longer codes. I just need this code performs well for both partial pivoting and like the code i given in the attached image. Just need to implement partial pivoting for only required $($not only given matrix$)$conditions$.$

My code:

import numpy as np

def eliminateCol$($A$,$ k$=0)$:

# guarantee that A is float type

if A$.$dtype.kind $!=\text{'}$f$\text{'}$ and A$.$dtype.kind $!=\text{'}$c$\text{'}$: return None

# load dimensions

dim$0,$dim$1=$ np$.$shape$($A$)$

# initialize outputs

swap $=$ np$.$identity$($dim$0,$dtype$=$float$)$

oper $=$ np$.$identity$($dim$0,$dtype$=$float$)$

# k $$ dim$1$

k $=$ k$\%$dim$1$

# if the column k is zero column, return

if A$[$:$,$k$].$any$()==$ False: return swap,oper

i$0=0$

if k $!=0$:

# find a row i$0$ whose left most k$-1$ entries are all zero

while i$0$ dim$0$:

if A$[$i$0,0$:k$].$any$()==$ False: break

i$0+=1$

# find a nonzero element A$[$i$,$k$]$ to use as a pivot

i $=$ i$0$;

while i $$ dim$0$:

if A$[$i$,$k$]!=0$: break

i$+=1$

if i $==$ dim$0$: return swap,oper

# swap the row i with the row i$0$

if i $!=$ i$0$: A$[[$i$0,$i$],]=$ A$[[$i$,$i$0],]$;swap$[[$i$0,$i$],]=$ swap$[[$i$,$i$0],]$

# row i$0$ is the pivot row and A$[$j$,$k$]$ is zero for i$0=0$:

if A$[$i$,$j$]!=0$:

quot $=$ A$[$i$,$j$]/$ A$[$k$,$j$]$

A$[$i$,$:$]=$ A$[$i$,$:$]-$ quot$*$A$[$k$,$:$]$

oper$[$i$,$k$]=-$quot

i$-=1$

return oper

def eliminateScale$($A$)$:

# guarantee that A is float type

if A$.$dtype.kind $!=\text{'}$f$\text{'}$ and A$.$dtype.kind $!=\text{'}$c$\text{'}$: return None

# load dimensions

dim$0,$dim$1=$ np$.$shape$($A$)$

# initialize outputs

oper $=$ np$.$identity$($dim$0,$dtype$=$float$)$

# find pivots

i $=0$

while i $$ dim$0$:

j $=0$

while j $$ dim$1$:

if A$[$i$,$j$]==0$: j$+=1$; continue

else:

oper$[$i$,$i$]=1/$A$[$i$,$j$]$

A$[$i$,$j:$]=$ A$[$i$,$j:$]/$A$[$i$,$j$]$

break

j$+=1$

i$+=1$

return oper

def echelon$\_$to$\_$rref $($A$)$:

# Perform Gaussian elimination on matrix A

for k in range$($A$.$shape$[1])$:

eliminateCol$($A$,$ k$)$

eliminateRow$($A$,$ k$)$

# Finally, scale the matrix

eliminateScale$($A$)$

return A

def get$\_$echelon$\_$form$($A$)$:

dim$0,$ dim$1=$ np$.$shape$($A$)$

for k in range$($min$($dim$0,$ dim$1))$:

# Eliminate below diagonal in column k

swap, oper $=$ eliminateCol$($A$,$ k$)$

return A

# Example Usage:

A $=$ np$.$array$([[0\mathrm{.}0,-1\mathrm{.}0,2\mathrm{.}0,8\mathrm{.}0],$

$[0\mathrm{.}0,0\mathrm{.}0,-1\mathrm{.}0,-11\mathrm{.}0],$

$[0\mathrm{.}0,2\mathrm{.}0,-1\mathrm{.}0,-3\mathrm{.}0]],$ dtype$=$float$)$

B $=$ np$.$array$([[1,2,3],$

$[4,5,6],$

$[7,8,9],$

$[10,11,12]],$ dtype$=$float$)$

echelon $=$ get$\_$echelon$\_$form$($B$.$copy$())$

reduced $=$ echelon$\_$to$\_$rref$($B$.$copy$())$

print$($A$)$

print$($echelon$)$

print$($reduced$)$