



 please provide the code in python (not just an explanation)
please provide the code in python (not just an explanation)
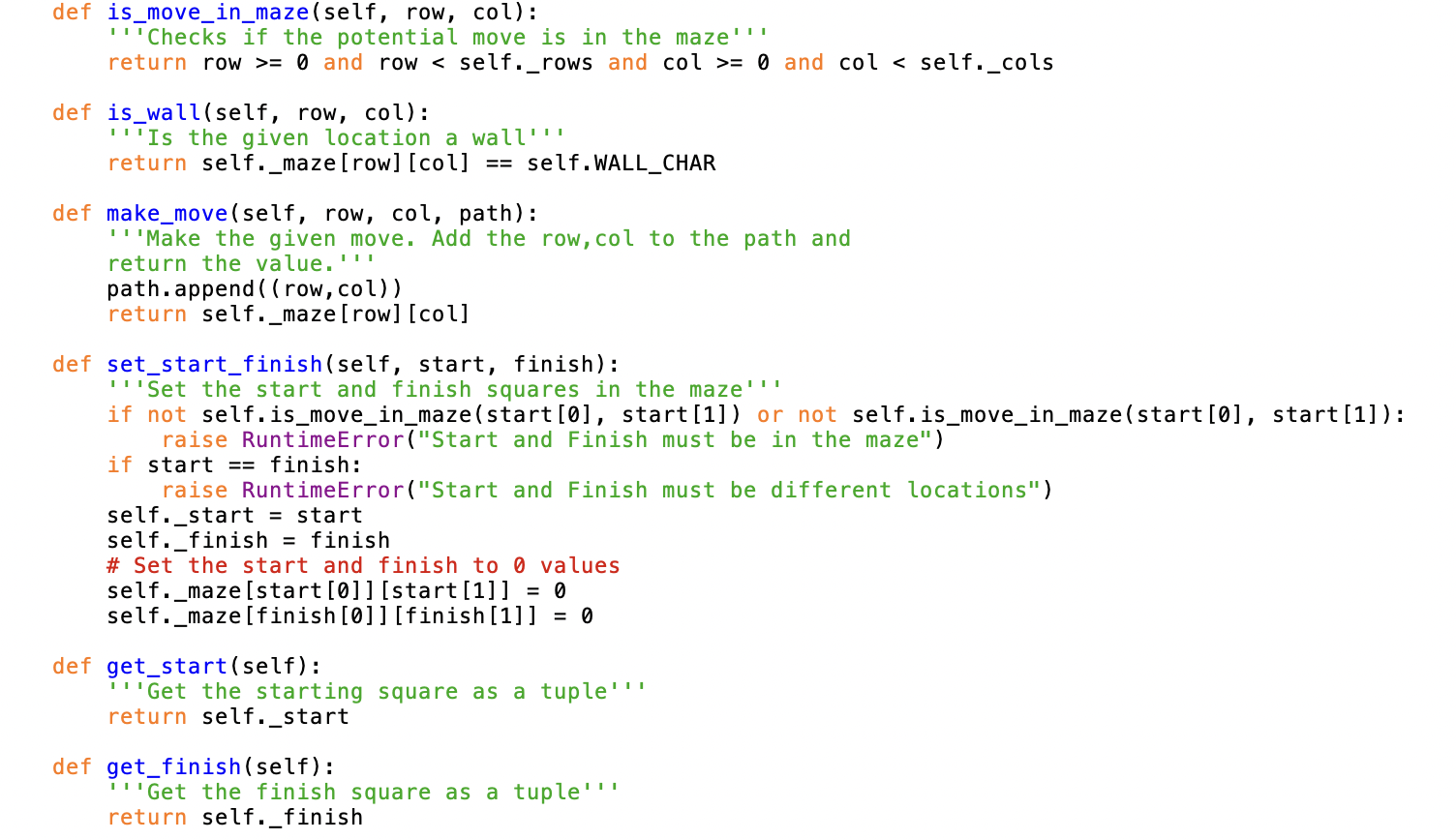
Mod 5 Homework - Recursion In this assignment, you will use recursion to solve a simple maze game. This game contains a two-dimensional grid of squares that serves as the maze. Each square in the maze is either a Point square (containing an integer value), a Wall square (denoted by ), the Start square ("S"), or the Finish square (" S). The goal is to find the path from Start to Finish that gathers the most "points." The path cannot pass through a wall nor can it double back on itself. The path can only flow horizontally or vertically between two adjacent squares. The path cannot flow diagonally. Here is an example of simple 55 maze. We will use the notation of (row, col) to reference a given square. Notice the Start is at (0,1) and the Finish is as (0,3 and the walls are marked by asterisks. The row and column labels are also provided to help you reference the correct square but are not considered part of the maze. Shown below is the best (and in this case, only) solution to this example maze. You can see the winning path marked by the @ character. If you count up all the point values originally occupied by the @ squares, the winning total is 49 (which is 5+2+3+9+1+3+1+4+7+3+8+2+1 ). Here is another example, this time a 33 maze that has three possible paths from Start to Finish. All three paths are valid, but the winning path is the one with the score of 16 . We will solve this puzzle using recursion, which allows the computer to try every permutation or possible path. The trick to writing a recursive function is to identify the "stop condition(s)" and then let your function try all options before reaching that stopping condition(s). You have been given the code for the Maze class (maze.py), complete with many attributes and methods that will be useful to your solution. You have also been given the shell of the Game class (game.py), which you will complete. An example test case is contained in test_game.py but you must add more test cases to ensure your recursive algorithm is correct for various edge cases. You can assume that the smallest maze will be 22, but mazes can be square or rectangular (e.g. 42,55,37). If the maze has no solution path from Start to Finish, your function should return a score of 1 and an empty List for the winning path. You must use recursion to find the best solution for any given maze. Submitting At a minimum, submit the following files: - game.py (adding your recursive function) - test_game.py (adding additional tests cases) - maze.py (do not alter any code in this file) Additionally, you must include any other files necessary for your code to run, such as modules containing data structures you wrote yourself. Do not import any modules you did not write yourself. The functionality added by external modules is one of the great things about python, but we restrict them for two reasons: - Some of them circumvent the purpose of these assignments, which is to develop basic algorithm design habits - Some of them are not supported by our Python install on Gradescope, making it impossible for us to run your code there (and thus slowing down our grading significantly) Students must submit individually by the due date (typically, Tuesday at 11:59 pm EST) to receive credit. limport random \# DO NOT modify any code in this class! class Maze( ): ''The actual grid of the maze that we are trying to solve." ' MINVAL =0# default MAXVAL =9 default WALL_CHAR = "*" def _init__(self, rows, cols): self cols = cols self.-minval = Maze.MINVAL self.-maxval = Maze.MAXVAL \# Testing method - the 2D list representing the maze can be set externally to facil def _set_maze(self, lst): def init_random (self, minval=MINVAL, maxval=MAXVAL): "'Initialize with random values. Optionally pass the min and max values for po \# 2D array: rows, cols self._maze = [ [random. randrange(minval, maxval) for i in range(self._cols)] for self._minval = minval self.-maxval = maxval def add_random_walls (self, percent_obstruction): "'Insert some random "walls" to make the maze non-trivial. The percent_obstruction (float in 0..1 ) determines the frequency of the walls in th maze. The more walls, the less winning paths and the less recursion will be needed for the solution. But it also means that some mazes will have no possible path from Start to Finish,', threshold = int ((self.maxval - self._minval) * percent_obstruction ) for row in range(self._rows): for col in range(self._cols): if self._maze [ row ][ col ]






 please provide the code in python (not just an explanation)
please provide the code in python (not just an explanation)





