Please refer to the screenshot :) thanks in advance!
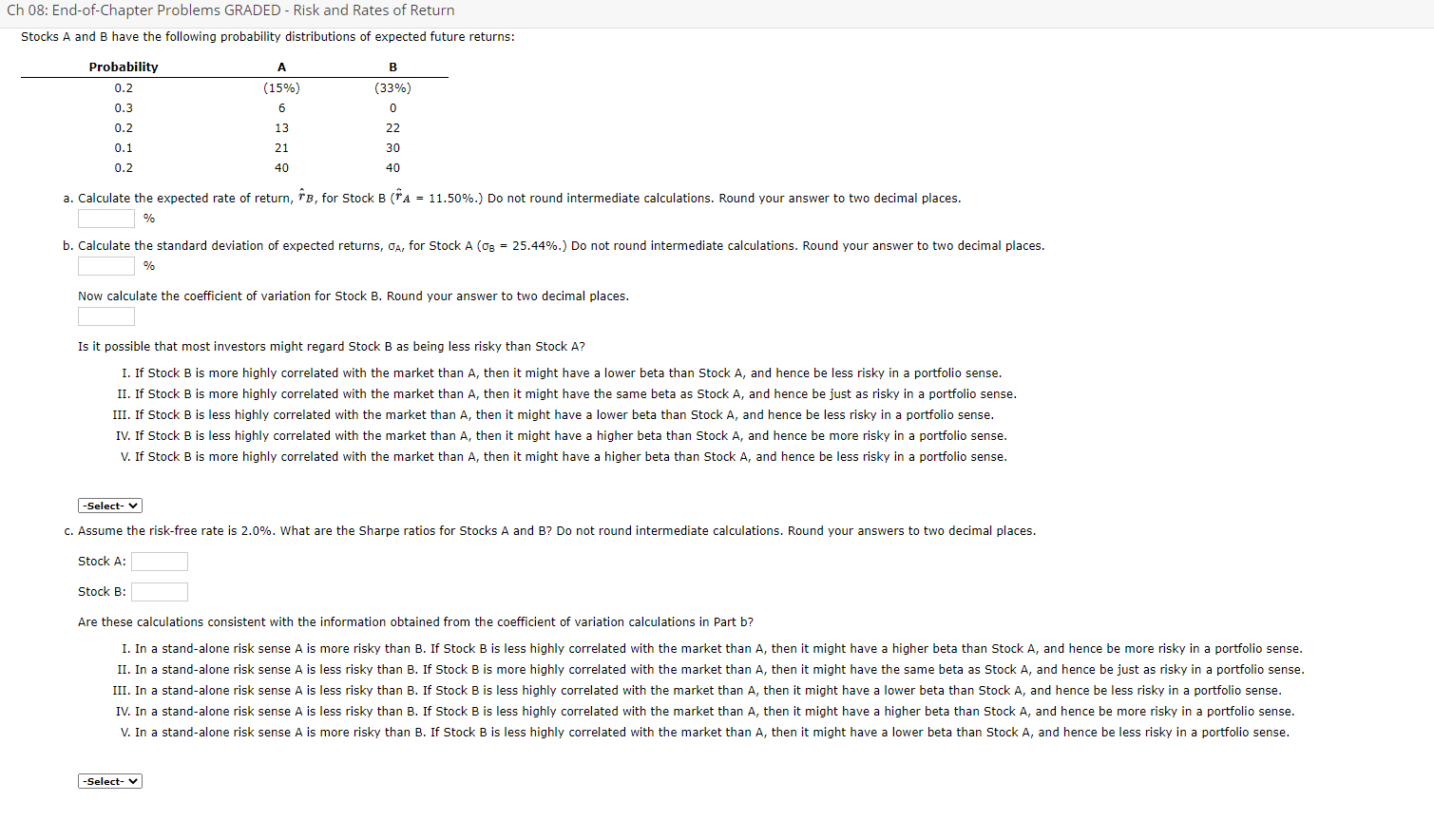
Ch 08: End-ofChapter Problems GRADED - Risk and Rates of Return Stoch A and B have the following probability distributions of expected future returns: Probability A B 0.2 (15%) (33%) 0.3 E l] 0.2 13 22 0.1 21 30 0.2 4D 40 a. Calculate the expected rate of return, 5'3, for Stock B (;'A : 11.50%.) Do not round inten'riediate calculations. Round your answer to two decimal places. % b. Calculate the standard deviation of expected returns, oA, for Stock A (on = 25.44%.) Do not round intermediate calculations. Round your answer to two decimal places. % Now calculate the coefficient of van'ation for Stock B. Round your answer to two decimal places. Is it possible that most investors might regard Stock B as being less nsky than Stock A? I. If Stock B is more highly correlated with the market than A, then it might have a lower beta than Stock A, and hence be less risky in a portfolio sense. II. If Stock B is more highly correlated with the market than A, then it might have the same beta as Stock A, and hence be just as risky in a portfolio sense. III. If Stock B is less highly correlated with the market than A, then it might have a lower beta than Stock A, and hence be less risky in a portfolio sense. IV. If Stock B is less highly correlated with the market than A, then it might have a higher beta than Stock A, and hence be more risky in a portfolio sense. V. If Stock B is more highly correlated with the market than A, then it might have a higher beta than Stock A, and hence be less risky in a portfolio sense. lad v c. Assume the risk-free rate is 2.0%. What are the Sharpe ratios for Stocks A and 87 Do not round intermediate calculations. Round your answers to two decimal places. Stock A: Stock B: Are these calculaons consistent with the information obtained from the coefcient of variation calculations in Pan b? I. In a standalone risk sense A is more risky than B. If Stock E is less highly correlated with the market than A, then it might have a higher beta than Stock A, and hence be more n'sky in a portfolio sense. II. In a stand-alone risk sense A is less risky than B. If Stock Bis more highly correlated with the market than A, then it might have the same beta as Stock A, and hence be just as risky in a portfolio sense. III. In a stand-alone risk sense A is less risky than B. If Stock B is less highly correlated with the market than A, then it might have a lower beta than Stock A, and hence be less risky in a portfolio sense. IV. In a standalone risk sense A is less risky than B. If Stock B is less highly correlated with the market than A, then it might have a higher beta than Stock A, and hence be more risky in a portfolio sense. V. In a stand-alone risk sense A is more risky than B. If Stock E is less highly correlated with the market than A, then it might have a lower beta than Stock A, and hence be less risky in a portfolio sense








