Question
PLEASE SHOW where and how w and Fh value found. Question 2 (20 pts). The device shown in the sketch is developed to measure the
PLEASE SHOW where and how w and Fh value found.
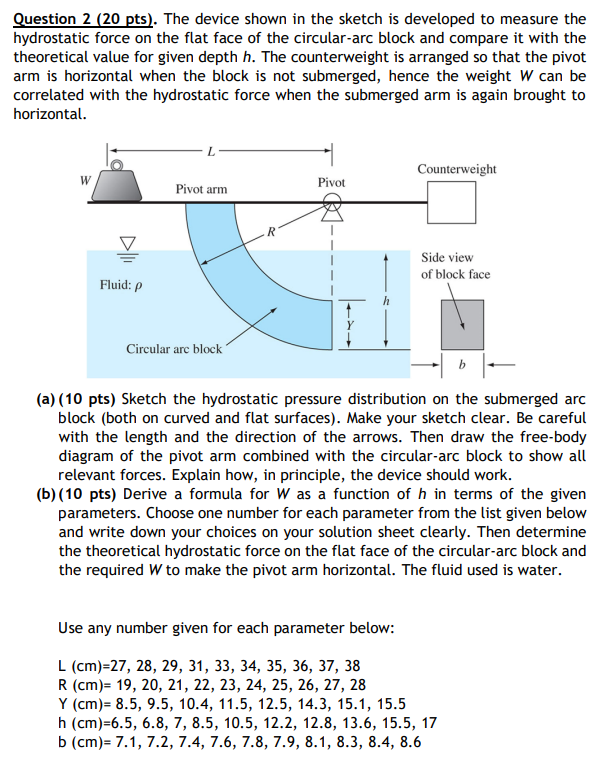
Question 2 (20 pts). The device shown in the sketch is developed to measure the hydrostatic force on the flat face of the circular-arc block and compare it with the theoretical value for given depth h. The counterweight is arranged so that the pivot arm is horizontal when the block is not submerged, hence the weight W can be correlated with the hydrostatic force when the submerged arm is again brought to horizontal. (a) (10 pts) Sketch the hydrostatic pressure distribution on the submerged arc block (both on curved and flat surfaces). Make your sketch clear. Be careful with the length and the direction of the arrows. Then draw the free-body diagram of the pivot arm combined with the circular-arc block to show all relevant forces. Explain how, in principle, the device should work. (b) (10 pts) Derive a formula for W as a function of h in terms of the given parameters. Choose one number for each parameter from the list given below and write down your choices on your solution sheet clearly. Then determine the theoretical hydrostatic force on the flat face of the circular-arc block and the required W to make the pivot arm horizontal. The fluid used is water. Use any number given for each parameter below: L (cm)=27, 28, 29, 31, 33, 34, 35, 36, 37, 38 R (cm)= 19, 20, 21, 22, 23, 24, 25, 26, 27, 28 Y (cm)= 8.5, 9.5, 10.4, 11.5, 12.5, 14.3, 15.1, 15.5 h (cm)=6.5, 6.8, 7, 8.5, 10.5, 12.2, 12.8, 13.6, 15.5, 17 b (cm)= 7.1, 7.2, 7.4, 7.6, 7.8, 7.9, 8.1, 8.3, 8.4, 8.6
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


