Please solve fully, do not waste my number of questions left for me, i need this and thank you

Problem: For the below question, use the Euler method. Show each calculation step clearly and draw the concentration profiles for the BOD and the toxicant is mandatory. Show limit values on the graphs and at the end discuss if the values meet the limitations or not. MATLAB is optional.

Part 1: An industry is considering equipping an existing tank (of volume V) as an activated sludge pretreatment system for treating their waste stream to meet the sewer discharge permit. This pretreatment system is expected to receive BOD and a nonbiodegradable, toxic chemical according to the schedule shown below, every two days:

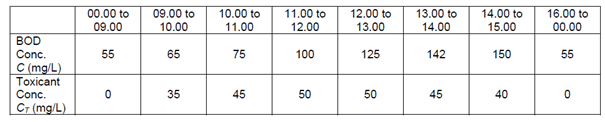
It has been found that if the concentration of the toxicant, CT, exceeds 25 mg/L in the bioreactor, it will be toxic to the primary strains in activated sludge. Additional available data are as follows: hydraulic retention times of existing tank = 0.6 day and biodegradation rate constant, k, assumed first order, = 3 day1 provided CT in the tank is less than 25 mg/L. The sewer discharge permit specifies a nominal limit of 20 mg/L BOD and a maximum limit of 30 mg/L BOD.

It is required to evaluate the feasibility of using the existing tank as an activated sludge unit to treat the waste to the required levels and to make recommendations to the industry. This problem is best solved by developing a mathematical model. First, a process model is developed based on the existing conditions:

where = (1/ + k); and the reaction rate constant k is defined as follows:

k = 3 day1 if CT 25 mg/L

The above MB equations are simple ODEs that can be solved analytically and implemented in a spreadsheet (e.g. Excel) if the inputs are either constants or simple functions of time. Equation solving and mathematical packages can be used if the inputs can be expressed as mathematical functions. In this example, the influent concentrations C and CT are arbitrary functions of time as shown in the schedule above; hence, numerical methods have to be used for solving them. Discuss if the concentration profiles you calculated meet the discharge permissible limits for the BOD and the toxicant.

Part 2: One option for meeting the discharge permit is to install a baffle to partition the tank to form two CMFRs in series (Section 5.23, where it was shown that multiple CMFRs in series are more efficient than a single one.) However, because the decrease in the toxicant concentration is due only to dilution (or washout), smaller tank volumes may result in inhibitory levels of the toxicant in one or both tanks. An optimal split of the total volume of the tank should, therefore, be found so that both criteria are adequately met. Or, in other words, adequate hydraulic detention time should be allowed in each tank so that the reaction can proceed to reduce the BOD concentration without being inhibited by the toxicant concentration. This involves some degree of trial and error, which can be done efficiently with a modified computer-based model. The MB equations can be readily derived as follows, with subscript 1 for the first reactor and subscript 2 for the second reactor:

Now, the equations are coupled ODEs with arbitrary inputs, and again, a numerical method has to be adapted for their solution.

\begin{tabular}{|l|c|c|c|c|c|c|c|c|} \hline & 00.00to09.00 & 09.00to10.00 & 10.00to11.00 & 11.00to12.00 & 12.00to13.00 & 13.00to14.00 & 14.00to15.00 & 16.00to00.00 \\ \hline BODConc.C(mg/L) & 55 & 65 & 75 & 100 & 125 & 142 & 150 & 55 \\ \hline ToxicantConc.CT(mg/L) & 0 & 35 & 45 & 50 & 50 & 45 & 40 & 0 \\ \hline \end{tabular} MB on toxicant: VdtdCT=QCT,inQCTdtdCT=1(CT,inCT) MB on BOD: VdtdC=QCinQCkVCdtdC=1Cin1CkC=1CinC MB equations for toxicant: dtdCT,1=11(CT,in,1CT,1) and dtdCT,2=21(CT,1CT,2) MB equations for BOD : dtdC1=11Cin,11C1 and dtdC2=21C12C2