Please solve the following in python ONLY PART A
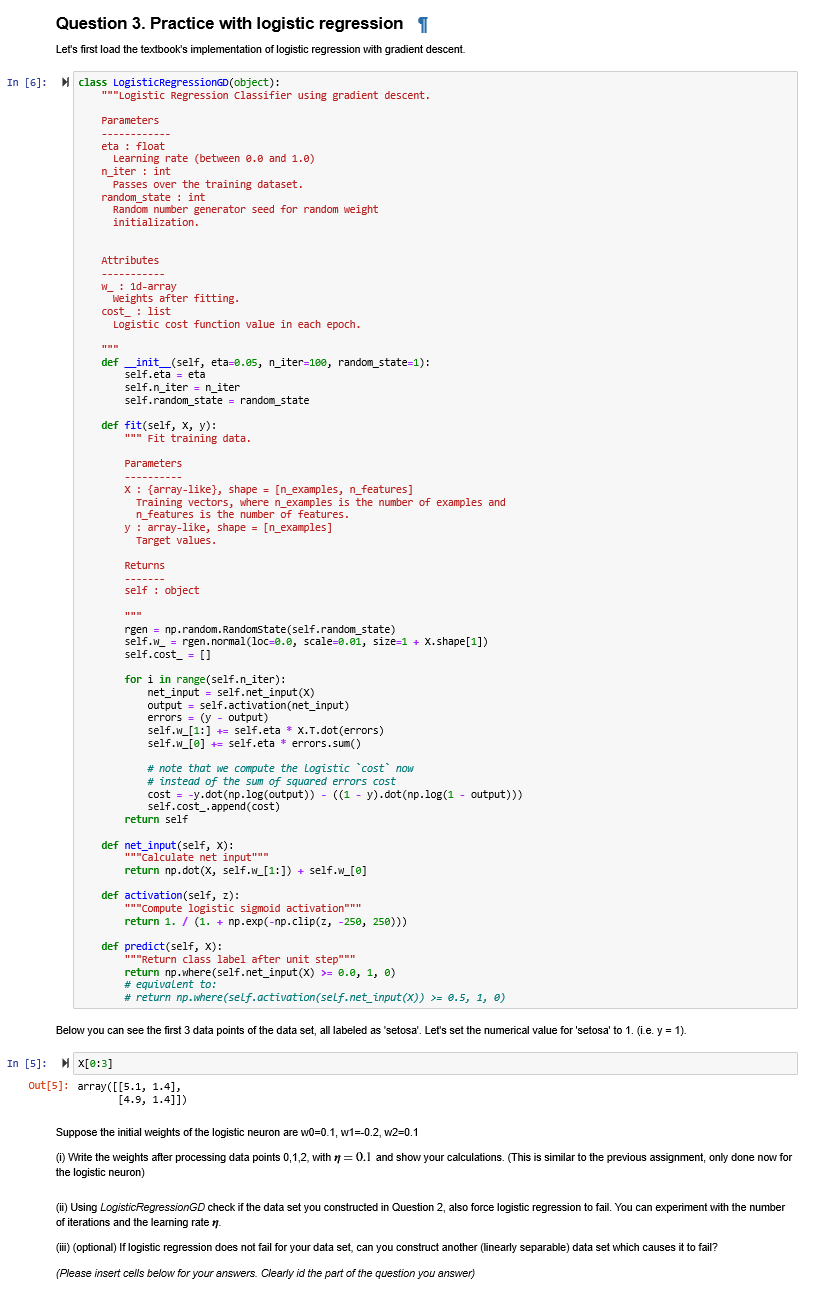
Question 3. Practice with logistic regression 1 Let's first load the textbook's implementation of logistic regression with gradient descent. In [6]: class LogisticRegressionGD (object): "Logistic Regression Classifier using gradient descent. Parameters eta : float Learning rate (between 8.and 1.0) n_iter : int Passes over the training dataset. random_state : int Random number generator seed for random weight initialization. Attributes W : 1d-array Weights after fitting. cost_ : list Logistic cost function value in each epoch. def __init__(self, eta=0.es, n_iter=180, random_state=1): self.eta = eta self.n_iter = n_iter self.random_state = random_state def fit (self, x, y): w Fit training data. Parameters X: {array-like), shape = [n_examples, n_features] Training vectors, where n_examples is the number of examples and n_features is the number of features. y : array-like, shape = [n_examples] Target values. Returns self : object rgen = np.random. RandomState(self.random_state) self.w_ = rgen.normal(loc=0.0, scale=0.61, size=1 + X.shape[1]) self.cost_ = [] for i in range(self.n_iter): net_input = self.net_input(X) output = self.activation(net_input) errors = (y - output) self.w_[1:] += self.eta * X.T.dot(errors) self.w_[@] += self.eta * errors.sum() # note that we compute the Logistic cost now # instead of the sum of squared errors cost cost = y.dot(np.log(output)) - ((1 - y).dot(np.log(1 - output) self.cost_.append(cost) return self def net_input (self,x): Calculate net input return np.dot(X, self.w_[1:]) + self.w_[@] def activation(self, z): "Compute logistic sigmoid activation return 1. / (1. + np.exp(-np.clip(z, -250, 250))) def predict(self,x): Return class label after unit step return np.where(self.net_input(x) >= 0.0, 1, 0) # equivalent to: # return np.where(self.activation(self.net_input(x)) >= 8.5, 1, 0) Below you can see the first 3 data points of the data set, all labeled as 'setosa'. Let's set the numerical value for 'setosa' to 1. (.e. y = 1). In [5]: x[8:3] Out[5]: array([[5.1, 1.4), [4.9, 1.4]]) Suppose the initial weights of the logistic neuron are wo=0.1, W1=-0.2, W2-0.1 (1) Write the weights after processing data points 0,1,2, with n=0.1 and show your calculations. (This is similar to the previous assignment, only done now for the logistic neuron) (ii) Using LogisticRegressionGD check if the data set you constructed in Question 2, also force logistic regression to fail. You can experiment with the number of iterations and the learning rate 1 (II) (optional) If logistic regression does not fail for your data set, can you construct another (linearly separable) data set which causes it to fail? (Please insert cells below for your answers. Clearly id the part of the question you answer) Question 3. Practice with logistic regression 1 Let's first load the textbook's implementation of logistic regression with gradient descent. In [6]: class LogisticRegressionGD (object): "Logistic Regression Classifier using gradient descent. Parameters eta : float Learning rate (between 8.and 1.0) n_iter : int Passes over the training dataset. random_state : int Random number generator seed for random weight initialization. Attributes W : 1d-array Weights after fitting. cost_ : list Logistic cost function value in each epoch. def __init__(self, eta=0.es, n_iter=180, random_state=1): self.eta = eta self.n_iter = n_iter self.random_state = random_state def fit (self, x, y): w Fit training data. Parameters X: {array-like), shape = [n_examples, n_features] Training vectors, where n_examples is the number of examples and n_features is the number of features. y : array-like, shape = [n_examples] Target values. Returns self : object rgen = np.random. RandomState(self.random_state) self.w_ = rgen.normal(loc=0.0, scale=0.61, size=1 + X.shape[1]) self.cost_ = [] for i in range(self.n_iter): net_input = self.net_input(X) output = self.activation(net_input) errors = (y - output) self.w_[1:] += self.eta * X.T.dot(errors) self.w_[@] += self.eta * errors.sum() # note that we compute the Logistic cost now # instead of the sum of squared errors cost cost = y.dot(np.log(output)) - ((1 - y).dot(np.log(1 - output) self.cost_.append(cost) return self def net_input (self,x): Calculate net input return np.dot(X, self.w_[1:]) + self.w_[@] def activation(self, z): "Compute logistic sigmoid activation return 1. / (1. + np.exp(-np.clip(z, -250, 250))) def predict(self,x): Return class label after unit step return np.where(self.net_input(x) >= 0.0, 1, 0) # equivalent to: # return np.where(self.activation(self.net_input(x)) >= 8.5, 1, 0) Below you can see the first 3 data points of the data set, all labeled as 'setosa'. Let's set the numerical value for 'setosa' to 1. (.e. y = 1). In [5]: x[8:3] Out[5]: array([[5.1, 1.4), [4.9, 1.4]]) Suppose the initial weights of the logistic neuron are wo=0.1, W1=-0.2, W2-0.1 (1) Write the weights after processing data points 0,1,2, with n=0.1 and show your calculations. (This is similar to the previous assignment, only done now for the logistic neuron) (ii) Using LogisticRegressionGD check if the data set you constructed in Question 2, also force logistic regression to fail. You can experiment with the number of iterations and the learning rate 1 (II) (optional) If logistic regression does not fail for your data set, can you construct another (linearly separable) data set which causes it to fail? (Please insert cells below for your answers. Clearly id the part of the question you answer)







