please solve this lab in c++ in virtual machine

I will be very thankful to you

I have edited it more information in the bottom.

please let me know if you still need more information.

inheritance.cpp

#include
	#include
	#include
	#include
	using namespace std;
	class Animal {
	public:
	Animal(string name) : name(name) {}
	virtual void talk() = 0; // pure virtual function
	string getName() const { return name; }
	private:
	// every Animal has a name
	string name;
	};
	class Cat : public Animal {
	public:
	Cat(string name) : Animal(name) {}
	void talk() override { cout
	};
	class Dog : public Animal {
	public:
	Dog(string name) : Animal(name) {}
	void talk() override { cout
	};
	int main() {
	auto c = make_shared("Lonzo");
	auto d = make_shared("Cisco");
	vector> v = {c, d};
	for (auto x : v) {
	cout getName()
	x->talk();
	}
	return 0;
	}

possibilities.rkt

#lang racket
	(define (print-possibilities unchosen-vars chosen-vars)
	(cond
	[(empty? unchosen-vars)
	;; base case: unchosen-vars is empty (we've chosen everything)
	;; print out the current chosen-vars
	(displayln (reverse chosen-vars))]
	[else
	;; recursive case: unchosen-vars is nonempty
	;; take one var out of unchosen-vars, and put it into chosen vars
	;; (trying each possibility)
	;; to extract the first thing in the list, we use first
	(define var (first unchosen-vars))
	;; to get everything except the first element, use rest
	(define rest-of-vars (rest unchosen-vars))
	;; try the tree possibilities for the var
	;; cons adds an element to the front of a list (and it also makes pairs)
	(print-possibilities rest-of-vars (cons `(,var "A") chosen-vars)) #| try A |#
	(print-possibilities rest-of-vars (cons `(,var "B") chosen-vars)) #| try B |#
	(print-possibilities rest-of-vars (cons `(,var "C") chosen-vars)) #| try C |# ]))
	(define (print-possibilities-prettier vars)
	(print-possibilities vars '()))
	;; initially, everything is unchosen and nothing is chosen
	(print-possibilities '("x" "y" "z") '())
	;; could also call the prettier version with:
	;; (print-possibilities-prettier '("x" "y" "z"))

smart-pointers

#include
	#include
	using namespace std;
	class C {
	public:
	int x;
	~C() { cout
	};
	int main() {
	// p points to a new int on the heap, with the value 42
	// unique_ptr is kind of like int*
	unique_ptr p = make_unique(42);
	cout
	unique_ptr p2 = make_unique();
	// unique_ptr p_2_copy = p2;
	// can't do the above because the ptr is supposed to be
	// unique (you can use move to move it, though)
	// The points inside p and p2 get deleted automatically for us right before
	// main returns
	shared_ptr p3 = make_shared(43);
	cout
	shared_ptr p4 = make_shared();
	shared_ptr p5 = p4; // it's okay to copy around shared_ptrs
	p5->x = 44;
	cout x
	return 0;
	}

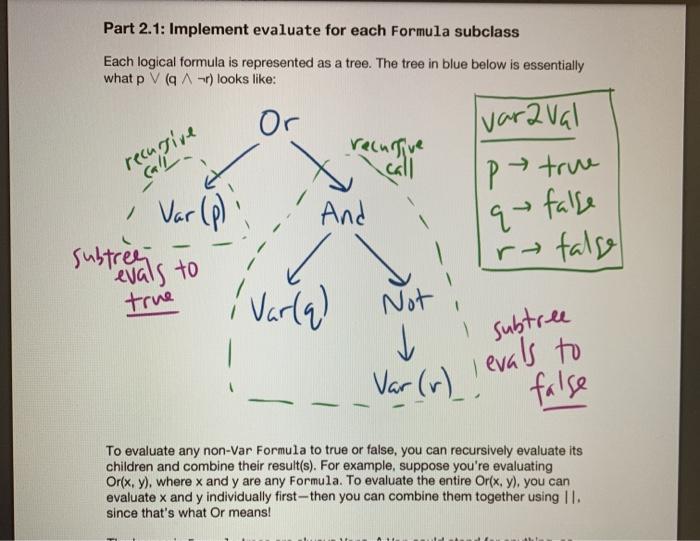
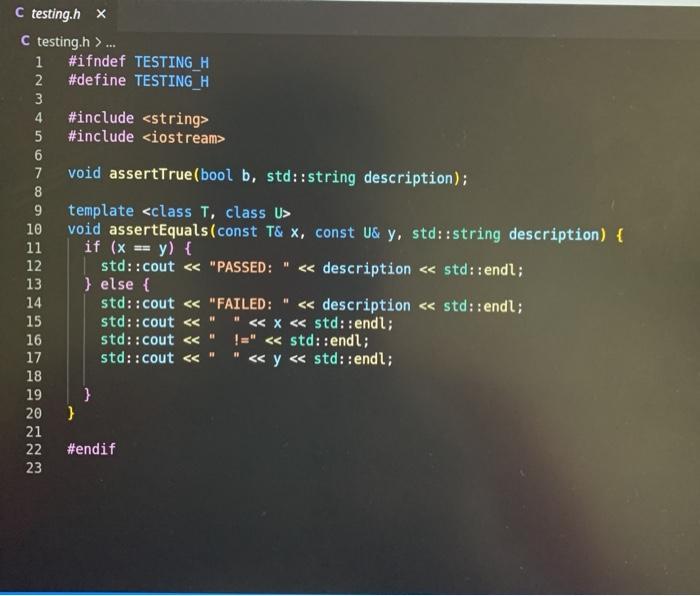
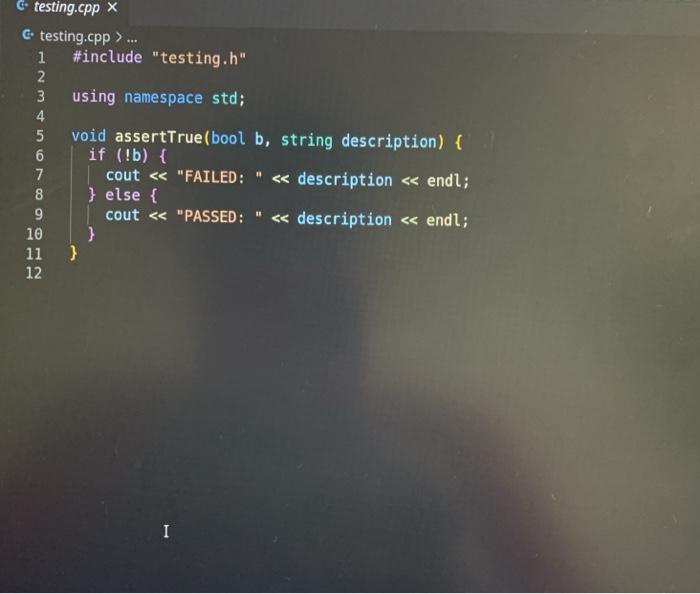
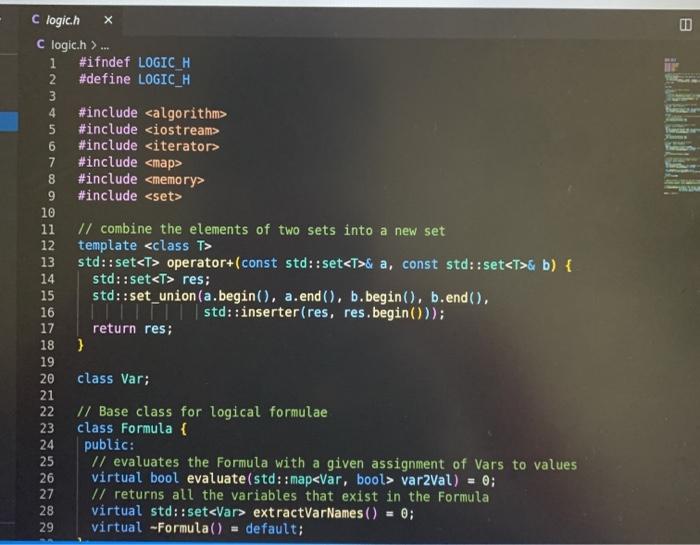
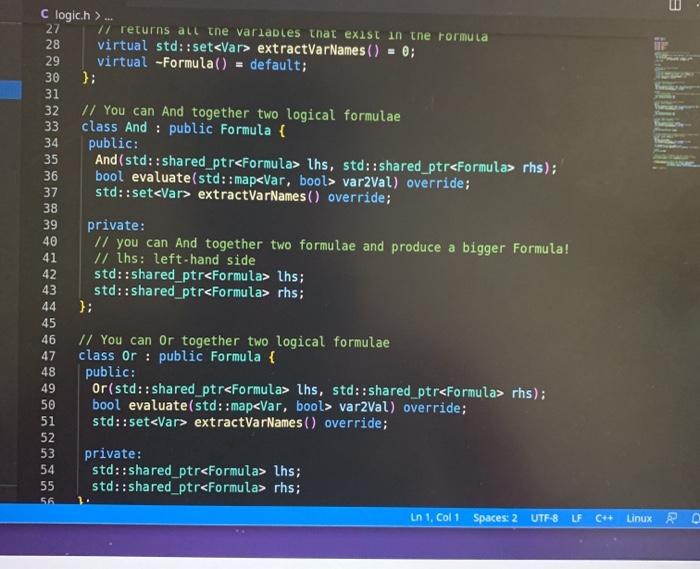
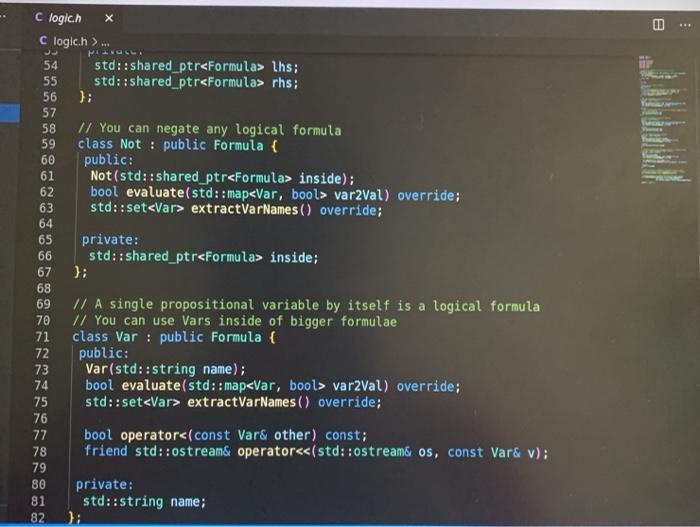
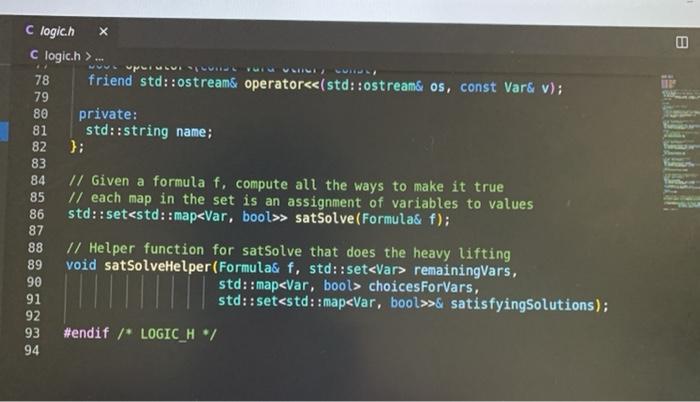
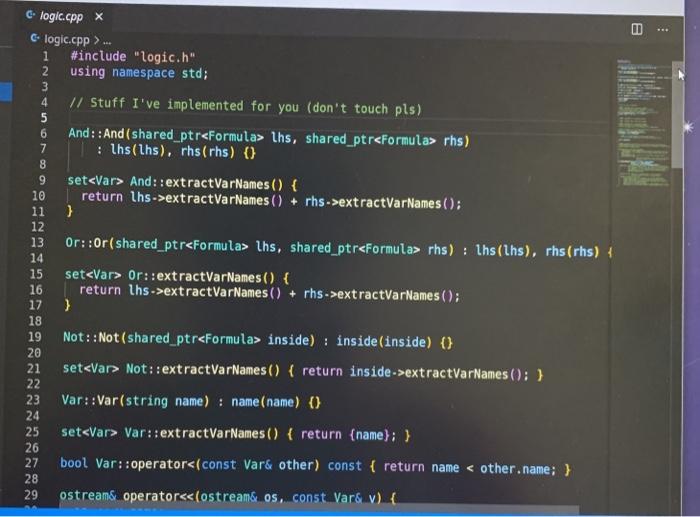
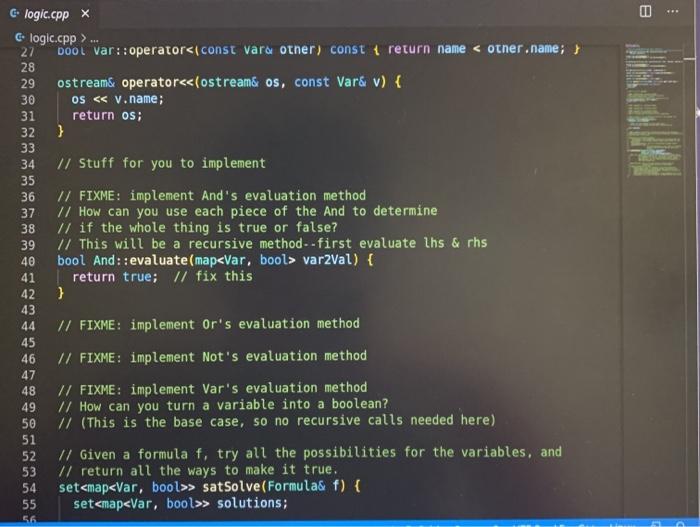
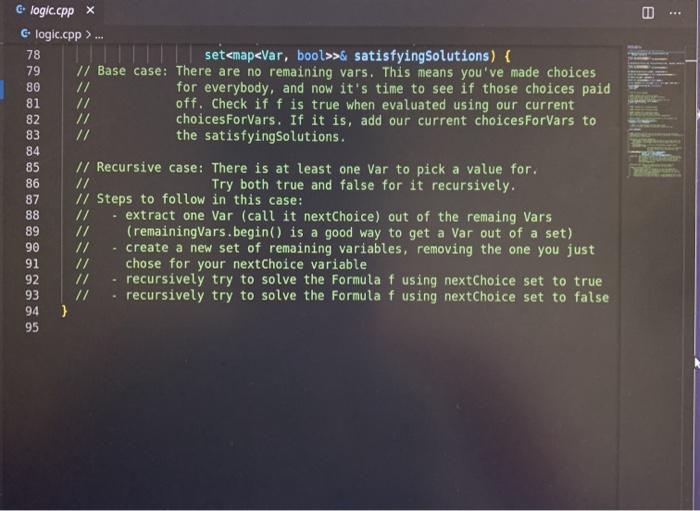
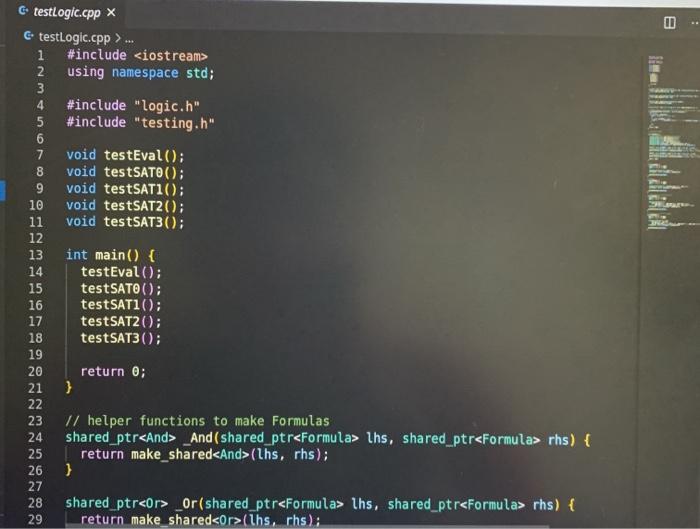
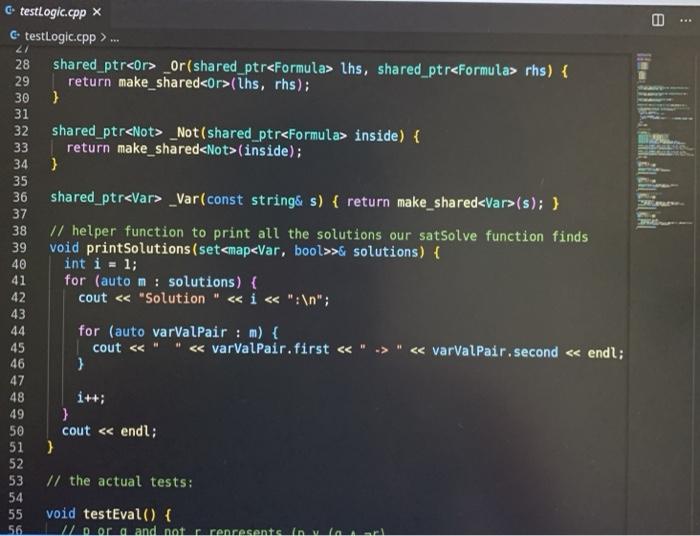
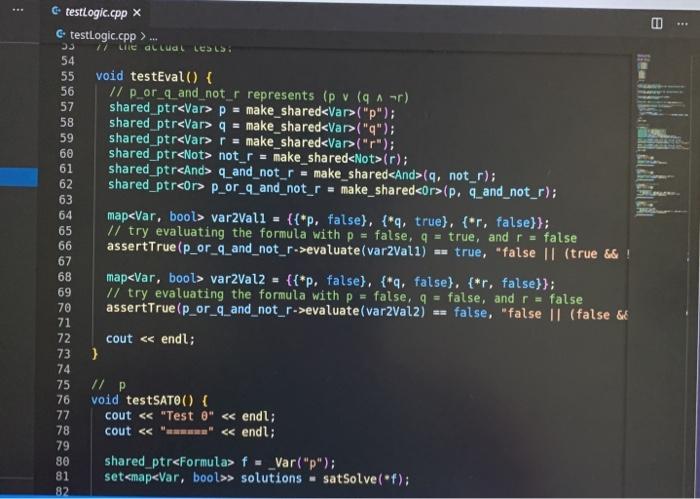
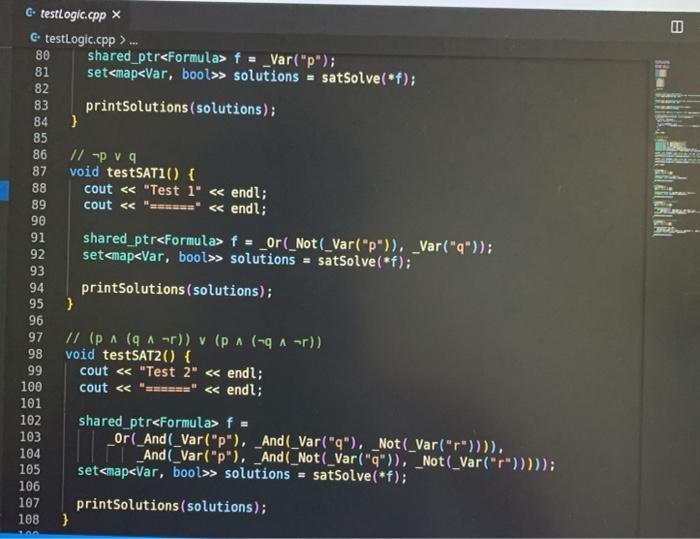
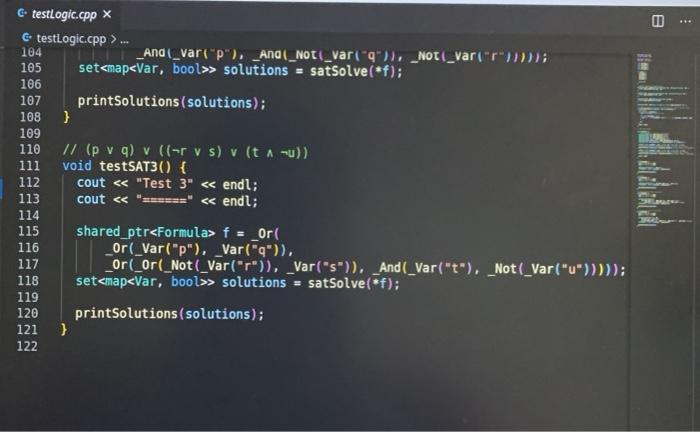
Lab 1: SAT Solving CSCI 26 Due date: February 11, 5pm Objectives: Practice using our logical skills with code Remember how trees, recursion, and inheritance work Part 1: Get the starter code First, get the latest starter code on your virtual machine by running the following command in the terminal: refresh-starter-code Next, cd into the folder where you store your class files (e.g../media/sf_CSCI/). Copy the starter code there with the following line: cp -R /starter-code/csci26/1ab01 . The dot at the end is important! This will make a lab01 folder in whatever directory you were in. Then, if you cd into that folder and run ls you should see the following files: $ ls expected-output.txt logic.h testing.cpp testLogic.cpp logic.cpp Makefile testing.h Now you're ready to start working. Part 2: SAT solve like there's no tomorrow Make sure to watch the introduction video that explains everything! You won't need to write more than 50 lines of code for this lab, but you'll have to think hard about every line. SAT solving is the process of taking a Boolean formula and determining whether or not it is satisfiable--that is, whether it is possible to set the variables just right to make the formula be true. For example, the formula p V (q^r) is satisfiable because you could set p = T. q = F, and r = F and the formula would evaluate to T. In this lab we want to find all the ways to make a formula satisfiable. Take a look at logic.h and testLogic.cpp, and notice how we're using subclasses of Formula to represent logical formulae. In particular, notice how I build the formula from above in testEval. Part 2.1: Implement evaluate for each Formula subclass Each logical formula is represented as a tree. The tree in blue below is essentially what p V (q) looks like: Or Ivaraval p> true recupive / la false ry talge Var (p) And subtres Varla) Var (r) ) ) evals to true Not I subtree evals to false To evaluate any non-Var Formula to true or false, you can recursively evaluate its children and combine their result(s). For example, suppose you're evaluating Or(x, y), where x and y are any Formula. To evaluate the entire Or(x, y), you can evaluate x and y individually first-then you can combine them together using II. since that's what Or means! The leaves in Formula trees are always Vars. A Var could stand for anything, so that is why we pass along the var2Val map (shown in green) when we call evaluate-the user must pick ahead of time what each variable's value is. Evaluating a Var, then, is as simple as looking up its value in the map. Implement the proper overridden evaluate method for each subclass of Formula. Part 2.2: Implement satSolve and satSolveHelper These two functions do the actual satisfiability checking, and they'll take the most work to get right. The goal of satSolve is to take a Formula, try every possible combination of values for every variable, and remember each combination that evaluated to true. A solution to a Formula is an assignment of variables that makes the Formula evaluate to true. The easiest way to do all this is with a recursive helper function. satSolveHelper takes four parameters: The Formula you're trying to SAT solve. The variables you haven't make choices for yet. The variables you have made choices for and the values you're currently trying for them). A reference to the set that contains all the satisfying solutions. Every time you find a new solution, you'll add it to this set. . Read the comments for an in-depth explanation of how the recursion needs to work. Here's a quick summary of what happens in each case: In the base case, you've made choices for each variable in the Formula f, and you're ready to try them out. If f evaluates to true with your current choices for variables, then you should add the solution to your set of solutions. In the recursive case, you're still guessing values for each variable. You'll take out a variable v that hasn't been assigned to yet, and make two different recursive calls--you do this because you need to try setting v to true and to false. o Each time you make a recursive call, the number of variables left to choose shrinks by one. That guarantees that you'll never get stuck in an infinite loop! When you make your initial call to satSolveHelper from inside satSolve, no decisions have been made yet. So, you'll start with a full set of remainingVars and an empty map of choices ForVars. You can compile with make testLogic and run with ./testLogic. Compare your output with expected-output.txt to know if you're on the right track. Part 3: Submit your code Once you're satisfied with your solution (or if you want to get some partial credit in), you can submit your code to the autograder. Do not submit and assume you got 100%-you may be unpleasantly surprised. Always check your grade. From your solution directory, submit your code to the autograder using the following command on the terminal: turnin lab01@csci26 logic.cpp The autograder will grade your code within 15-30 minutes. If it's not working, please yell at Lawton to fix it. Run refresh-grades to download your updated grades, and view-grades to look at them. You may resubmit as much as you want before the due date. Rubric Rubric Item Points (24 pts total) The evaluate tests pass 4 pts (2 for each test) 20 pts (5 for each test) The satSolve tests pass UAWN C testing.hx C testing.h>... i #ifndef TESTING_H 2 #define TESTING_H 3 4 #include 5 #include 6 7 void assertTrue(bool b, std::string description); 8 9 template 10 void assertEquals(const T& X, const u& y, std::string description) { 11 if (x == y) { 12 std::cout ... 1 #include "testing.h" 2 3 using namespace std; 4 5 void assertTrue(bool b, string description) { 6 if (!b) { 7 cout ... 1 #ifndef LOGIC_H 2 #define LOGIC_H 3 4 #include #include 7 #include