please solve with jupyternotebook (anaconda)

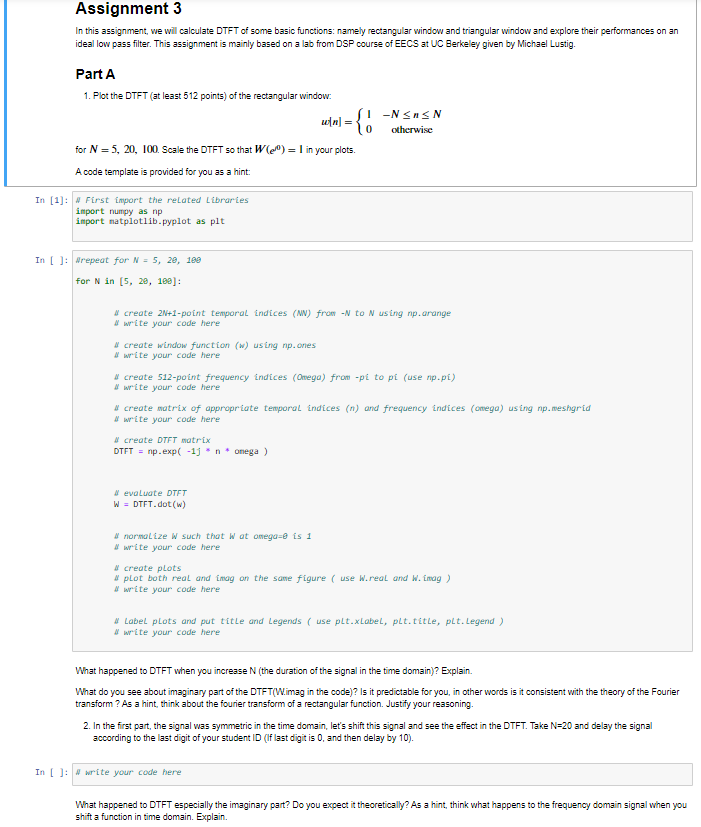
In this assignment, we will calculate DTFT of some basic functions: namely rectangular window and triangular window and explore their performances on an ideal low pass filter. This assignment is mainly based on a lab from DSP course of EECS at UC Berkeley given by Michael Lustig. Part A 1. Plot the DTFT (at least 512 points) of the rectangular window: w[n]={10NnNotherwise for N=5,20,100. Scale the DTFT so that W(ej0)=1 in your plots. A code template is provided for you as a hint: In First import the related Librarties import numpy as np import natplotlib.pyplot as p1t Nrepeat for N=5,20,160 for N in [5,29,100] : M create 2N+1point temporal indices (MN) from N to N using np.arange \# write your code here II create window function (w) using np.ones \#" write your code here \#" create 512-point frequency indices (Omega) frow -pi to pi (use np.pi) write your code here " create matrix of appropriate temporal indices (n) and frequency indices (onega) using np.meshgrid U write your code here "create DTFT matrix DTFT =npexp(1jn onega ) " evaluate DTFT W= DTFT. dot (W) U normalize W such that W at amega= is 1 * write your code here A create plots "plot both real and inag an the same figure (use W.real and W. imag) " write your code here "Label plots and put title and Legends ( use plt.xLabeL, plt.title, pLt. Legend) " write your code here What happened to DTFT when you increase N (the duration of the signal in the time domain)? Explain. What do you see about imaginary part of the DTFT(W.imag in the code)? Is it predictable for you, in other words is it consistent with the theory of the Fourier transform? As a hint, think about the fourier transform of a rectangular function. Justify your reasoning. 2. In the first part, the signal was symmetric in the time domain, let's shif this signal and see the effect in the DTFT. Take N=20 and delay the signal according to the last digit of your student ID (If last digit is 0 , and then delay by 10). In write your code here What happened to DTFT especially the imaginary part? Do you expect it theoretically? As a hint, think what happens to the frequency domain signal when you shift a function in time domain. Explain. In this assignment, we will calculate DTFT of some basic functions: namely rectangular window and triangular window and explore their performances on an ideal low pass filter. This assignment is mainly based on a lab from DSP course of EECS at UC Berkeley given by Michael Lustig. Part A 1. Plot the DTFT (at least 512 points) of the rectangular window: w[n]={10NnNotherwise for N=5,20,100. Scale the DTFT so that W(ej0)=1 in your plots. A code template is provided for you as a hint: In First import the related Librarties import numpy as np import natplotlib.pyplot as p1t Nrepeat for N=5,20,160 for N in [5,29,100] : M create 2N+1point temporal indices (MN) from N to N using np.arange \# write your code here II create window function (w) using np.ones \#" write your code here \#" create 512-point frequency indices (Omega) frow -pi to pi (use np.pi) write your code here " create matrix of appropriate temporal indices (n) and frequency indices (onega) using np.meshgrid U write your code here "create DTFT matrix DTFT =npexp(1jn onega ) " evaluate DTFT W= DTFT. dot (W) U normalize W such that W at amega= is 1 * write your code here A create plots "plot both real and inag an the same figure (use W.real and W. imag) " write your code here "Label plots and put title and Legends ( use plt.xLabeL, plt.title, pLt. Legend) " write your code here What happened to DTFT when you increase N (the duration of the signal in the time domain)? Explain. What do you see about imaginary part of the DTFT(W.imag in the code)? Is it predictable for you, in other words is it consistent with the theory of the Fourier transform? As a hint, think about the fourier transform of a rectangular function. Justify your reasoning. 2. In the first part, the signal was symmetric in the time domain, let's shif this signal and see the effect in the DTFT. Take N=20 and delay the signal according to the last digit of your student ID (If last digit is 0 , and then delay by 10). In write your code here What happened to DTFT especially the imaginary part? Do you expect it theoretically? As a hint, think what happens to the frequency domain signal when you shift a function in time domain. Explain