Please use Matlab
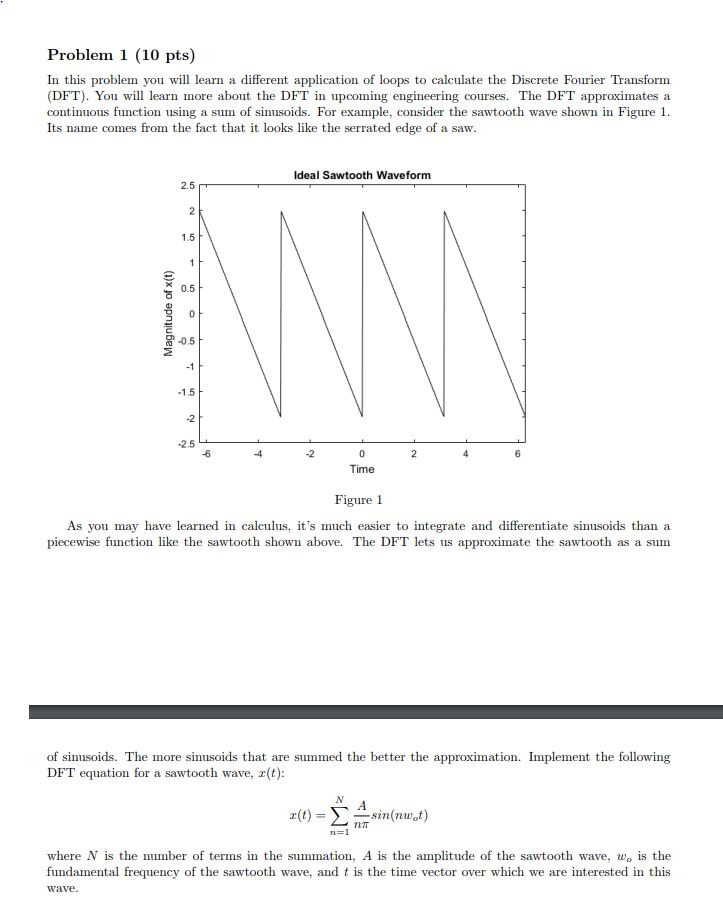

Problem 1 (10 pts) In this problem you wll learn a different application of loops to calculate the Discrete Fourier Transform (DFT). You will learn more about the DFT in upcoming engineering courses. The DFT approximates a continuous function using a sum of sinusoids. For example, consider the sawtooth wave shown in Figure 1 Its name comes from the fact that it looks like the serrated edge of a saw. Ideal Sawtooth Waveform 2.5 1.5 0.5 0.5 1.5 -2 2.5 Time Figure 1 As you may have learned in calcuus, it's much easier to integrate and differentiate sinusoids than a function like the sawtooth shown above. The DFT lets us approximate the sawtooth as a sum of sinusoids. The more sinusoids that are summed the better the approximation. Implement the following DFT equation for a sawtooth wave, z(t) z(t)- where N is the number of terms in the summation, A is the amplitude of the sawtooth wave, wo is the fundamental frequency of the sawtooth wave, and t is the time vector over which we are interested in this wave of sinusoids. The more sinusoids that are summed the better the approximation. Implement the following DFT equation for a sawtooth wave, z(t) where N is the number of terms in the summation, A is the amplitude of the sawtooth wave, wo is the fundamental frequency of the sawtooth wave, and t is the time vector over which we are interested in this wave. a) Setup the inputs to the equation based on the information in Figure 1. The time vector should be from-2 to 2 with a step size of 0.02. Based on Figure 1, the amplitude of the sawtooth wave is 2. and the fundamental frequency is 2 (two cycles per 2) b) Use a for loop to calculate x(t) in Equation 1 for N 5. c) Use a while loop to calculate x(t) in Equation for N 25 d) Plot r(t) vs t for N 5 and N 25 as subplots, one on top of the other (two rows, one column) Label the x-axis Magnitude and the y-axis Time. Adjust the x-axis to-2 to 2 and the y-axis to 2.5 to 2.5. Problem 2 (10 pts) Below shows the Taylor Series equivalent of the inverse tangent of x: z2n+1 2n +1 3 5 79 for -1 r You will use MATLAB to approximate arctan(z) using the above Taylor Series. In MATLAB, the upper bound of the summation cannot be set to infinity, instead you have to choose a value to stop evaluating the Taylor Series. The value you will use is N 10 a) Calculate the Taylor Series expansion of arctan(0.5) using upper bound N 10 using a while loop b) Calculate the Taylor Series expansion of arctan (0.5) using upper bound N = 10 using a or loop. Set c) Does the while loop and the for loop Taylor series expansion approximately give the sa? Give d) Calculate the percent error by comparing the result of the Taylor Series of arctan(0.5) with the actual Set the result equal to the variable T1 the result equal to the variable T2 you answer as a comment value. e) Use tic and toc to measure the time required to calculate arctan(0.5) using the built-in function arctan), using the for loop, and using the while loop. Using fprintf, display the time elapsed for each. Hint: suppress the statement automatically displayed when using tic and toc by setting toc equal to a variable.) Remember to include units! Please submit one .m file for this assignm the same .m file ent. The solutions to both problems should be in








