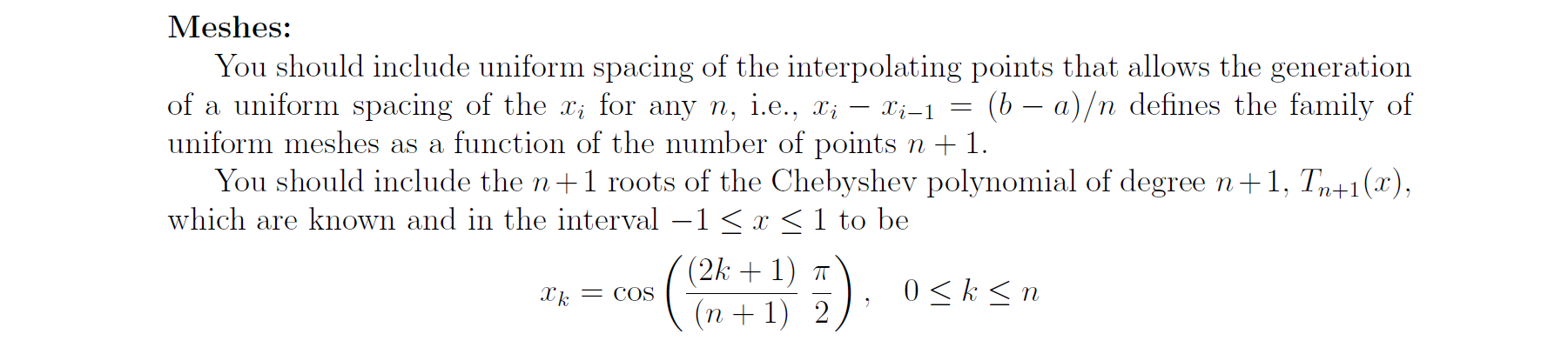Please write a C++ program.




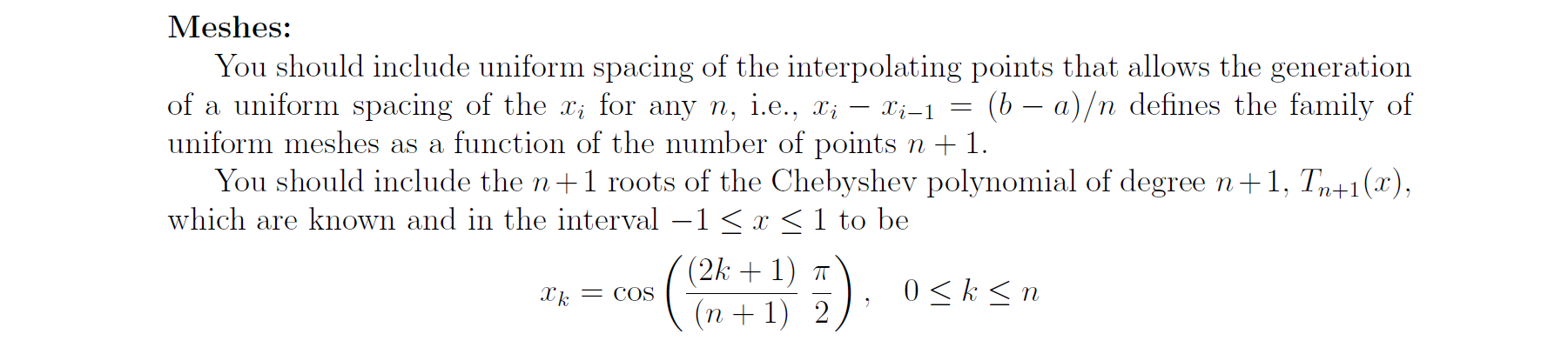

Algorithms Required: Assume you are given distinct points a = 80, ..., In = b, on the interval (a, b) and a function f(x) defined on the interval. Implement the following algorithms 1. Newton form of the interpolating polynomial:. There should be two routines. The first computes the required divided differences and returns them for use by the second which evaluates the Newton form of the polynomial for a given x value. You may find it useful to implement this so that a set of x values can be given as input and the set of the values of the polynomial at those points is returned. In your solutions denote this polynomial Na(2) when it has degree d. This first routine should accept any mesh of x; points on the interval of interest, i.e., it is not restricted to any specific set of r; values like Chebyshev points or equidistant points. The second routine should accept any set of x values on which the polynomial is to be evaluated including points on the mesh used to generate the divided differences. 2. Piecewise interpolating polynomial: The routine for the piecewise interpolating polynomial 98(1), on [a, b] where the degree s should support choosing s to be 1 or 2, i.e., piecewise linear or piecewise quadratic. Code Comments: Your codes should be able to run in single or double precision (assumed to be IEEE standard FP). Your codes must be efficient in time and space and make sure you discuss these aspects of your implementations. Compute the divided differences using the divided difference table approach. Your implementation must be efficient in storage, i.e., O(n) space. Therefore, you must decide what form of Na(c) you will use, i.e., the one starting with fo and adding the values at 11,...,xn-1, In or the one starting with fr and adding the fi values at An-1,...,11, 20. In either case when computing the divided difference table your algorithm must use only O(n) work space and should not store the entire table. The piecewise interpolating polynomial algorithm should use a simple selection mecha- nism for the degree, i.e., do not write separate routines for each degree in some assumed range of degrees. The piecewise interpolating polynomials must be continuous. So the mesh of interpo- lation points used in each subinterval must include the two end points. Therefore, the piecewise linear polynomial, 91(2), will define a linear polynomial, P1i(2) for each of the n intervals, [li, l'i+1], i = 0,...,n 1. The piecewise quadratic polynomial, g2(x), will define a quadratic polynomial, P2, i(x) for of the n/2 intervals wit n = 2k, i.e., n is assumed to be even. The intervals are (C21, T2i+2), i = 0,..., (n/2) 1. Note that the points with the odd indices are contained in these intervals. The low degree of s = 1, 2 implies that 1 or 2 divided differeces are required per interval. You may implement this simple computation separately from the Newton divided difference polynomial code above that must handle a much wider range of degree and table size. The piecewise polynomial codes must be able to specify a general mesh of points and a uniform mesh of points. When investigating the performance and correctness of your codes: . You should carefully choose the functions to interpolate and demonstrate the predicted error holds for both global and piecewise interpolants. Recall the error should be very near zero at the interpolation points. To approximate ||| (x) 9(2)||- and ||| (x) - Na(2)||20, sample f(x) and the approx- imating function at a large number of points, zi, in the interval and take the largest value of the magnitude of the difference between f(zi) and the approximating function at zz. When the number of z; is sufficiently large this will give a good approximation of the error. Tasks: Task 1 Discuss the complexity of preprocessing and evaluation for each method. Note this complexity analysis should include the search for the interval in which the value resides for piecewise interpolating and how assumptions about the mesh can influence the complexity of the search Task 2 It is known from the error bounds that N.(r) is identical to f(x) as long as f(0) is a polynomial of degree less than or equal to d. Use this as one debugging/validation test for your Newton interpolating polynomial code by producing Na(r) for d=1,2, ...c where fr) is a polynomial of degree c. Do this for many such f(c) and present the results in such a way that it is convincing that your code reproduces polynomials correctly. Task 3 Apply the error bounds of the notes for piecewise polynomial interpolation with degrees 15 s