please write in assembly language to add two floating point values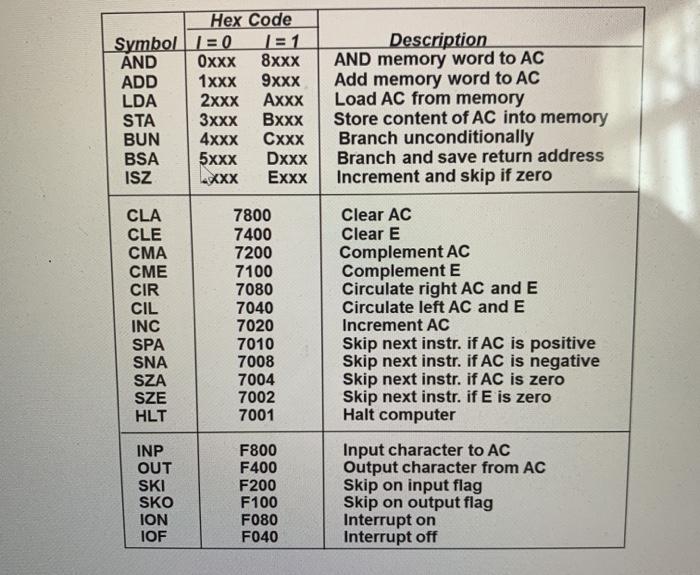

Hex Code Symbol 1 = 0 1 = 1 AND Oxxx 8xxx ADD 1xxx 9xxx LDA 2xxx Axxx STA 3XXX Bxxx BUN 4xxx Cxxx BSA 5xxx Dxxx ISZ XXX Exxx Description AND memory word to AC Add memory word to AC Load AC from memory Store content of AC into memory Branch unconditionally Branch and save return address Increment and skip if zero CLA CLE CMA CIR CIL INC SPA SNA SZA SZE HLT 7800 7400 7200 7100 7080 7040 7020 7010 7008 7004 7002 7001 Clear AC Clear E Complement AC Complement E Circulate right AC and E Circulate left AC and E Increment AC Skip next instr. if AC is positive Skip next instr. if AC is negative Skip next instr. if AC is zero Skip next instr. if E is zero Halt computer Input character to AC Output character from AC Skip on input flag Skip on output flag Interrupt on Interrupt off INP OUT SKI SKO F800 F400 F200 F100 F080 F040 ION IOF Write assembly language programs to perform each of the following floating-point operations on two input floating point numbers A and B: 1. Compute C-A+B and produce a normalized floating point result 2. Compute D-AXB and produce a normalized floating point result D (notice that in order to be able to perform this operation, you need to implement a subroutine that performs multiplication of two unsigned integers) You can make the following assumptions: 1. The mantissa's are unsigned (i.e., no negative values) 2. A and B are non-zero values and A is greater than B 3. The mantissa of input values A and B require no more than 8-bits (i.e., they are smaller than 256. Therefore, their multiplication will not result in a value that requires more than 16 bits. 4. No overflow or underflow could occur. Therefore, you can ignore checking for these. Add Algorithm 1. Align the binary point of the two values by shifting the mantissa of the smaller value (1.e. B) right by a number of positions equal to the difference between exponents. With this you can imagine that both values have the same exponents and, therefore, the locations of their binary points are aligned. Make sure that for the first position shift, you should shift in a "I" value (the implicit most significant bit). 2. Compute the result a. The result mantissa of the result is the addition of both mantissa's b. The result exponent is the common exponent after aligning the binary point, which is the exponent of A 3. Normalize the result by shifting the result right by one position (if needed) and adjusting (incrementing) the exponent. Notice that considering the above assumptions, you only need to do shift the result by a maximum of one position if there is a carry when you add the mantissa's