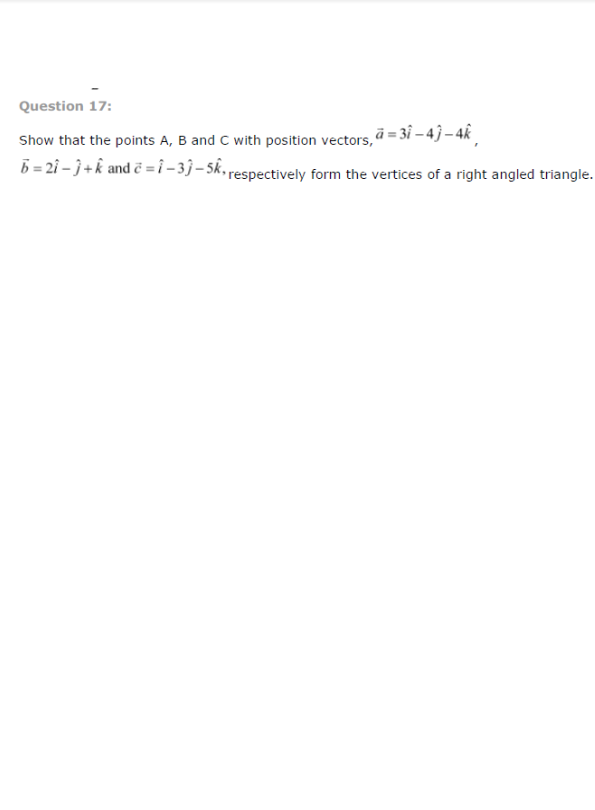
Question
Practice estimation: Estimation can help you quickly approximate the answer to a math problem. Practice estimation regularly to improve your accuracy. TUTORS READ THIS: Can
Practice estimation: Estimation can help you quickly approximate the answer to a math problem. Practice estimation regularly to improve your accuracy.
TUTORS READ THIS:
Can this tutor "prodindo" answer this questions because he did my last ASSIGMENT and he knows about this topic can you guys skip it till it goes to him THANK YOU because he knows this topic and what to do .
Understand the problem: One of the most important steps in solving a math problem is to understand what the problem is asking you to do. Read the problem carefully and make sure you understand what is being asked. Look for keywords and phrases that indicate what operation(s) you need to perform to solve the problem. Identify any unknowns or variables that you will need to find or calculate.
Choose a strategy: Once you understand the problem, choose a strategy for solving it. There are many different strategies you can use, such as drawing a diagram, using algebraic equations, or working backwards. Choose a strategy that you are comfortable with and that is appropriate for the problem at hand.
Plan your solution: Before you start solving the problem, plan out your solution. This can include sketching a diagram, writing down any equations or formulas you will need to use, and breaking the problem down into smaller, more manageable parts. Planning your solution will help you avoid mistakes and make the problem easier to solve.
Show your work: When solving a math problem, it is important to show your work. Write down each step of the solution and show how you arrived at your answer. This not only helps you keep track of your progress, but also makes it easier to check your work and identify any mistakes you may have made.
Check your answer: After you have solved the problem, check your answer to make sure it is correct. Double-check your calculations and make sure you have answered the question that was asked. If you are using a calculator, make sure you have entered the numbers and operations correctly.
Practice: The more you practice solving math problems, the better you will become at it. Practice regularly by working through practice problems or completing assignments. This will help you build your skills and confidence in solving math problems.
Seek help when needed: If you are struggling to solve a math problem, don't be afraid to seek help. Talk to your teacher or a tutor, or join a study group to get help from your peers. There are also many online resources and forums where you can ask questions and get help from experts in the field.
Understand the concepts: To become proficient in solving math problems, it is important to have a solid understanding of the underlying concepts. Make sure you understand the basic principles of arithmetic, algebra, geometry, and other branches of math. This will make it easier to solve problems and will help you identify when you are making mistakes.
Be patient: Solving math problems can be challenging and frustrating at times. It is important to be patient and take your time when working through a problem. Rushing through a problem can lead to mistakes and errors, so take the time you need to work through each step carefully.
Practice critical thinking: Math problems often require critical thinking skills, such as analyzing information, making connections between different concepts, and identifying patterns. To become proficient in solving math problems, practice your critical thinking skills by working through complex problems and exploring different strategies for solving them.
Simplify the problem: If the problem seems overwhelming, try simplifying it by removing unnecessary information or breaking it down into smaller parts.
Use examples: Using examples can help you better understand the problem and come up with a solution.
Be organized: Keep your work organized and tidy, making it easier to double-check your calculations and identify any mistakes.
Practice good time management: Managing your time well can help you avoid rushing through the problem and making mistakes.
Read the instructions carefully: Make sure you understand any specific instructions or guidelines that are provided with the problem.
Identify patterns: Identifying patterns in the problem can help you come up with a solution more easily.
Look for shortcuts: Sometimes there are shortcuts or tricks to solving a math problem. Look for these and use them if possible.
Work with a partner: Working with a partner can help you solve problems more quickly and can also provide a different perspective on the problem.
Keep an open mind: Sometimes the solution to a problem may not be immediately obvious. Keeping an open mind and considering different approaches can help you find a solution.
Learn from your mistakes: If you make a mistake, don't get discouraged. Instead, use it as an opportunity to learn and improve your problem-solving skills.

















Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


