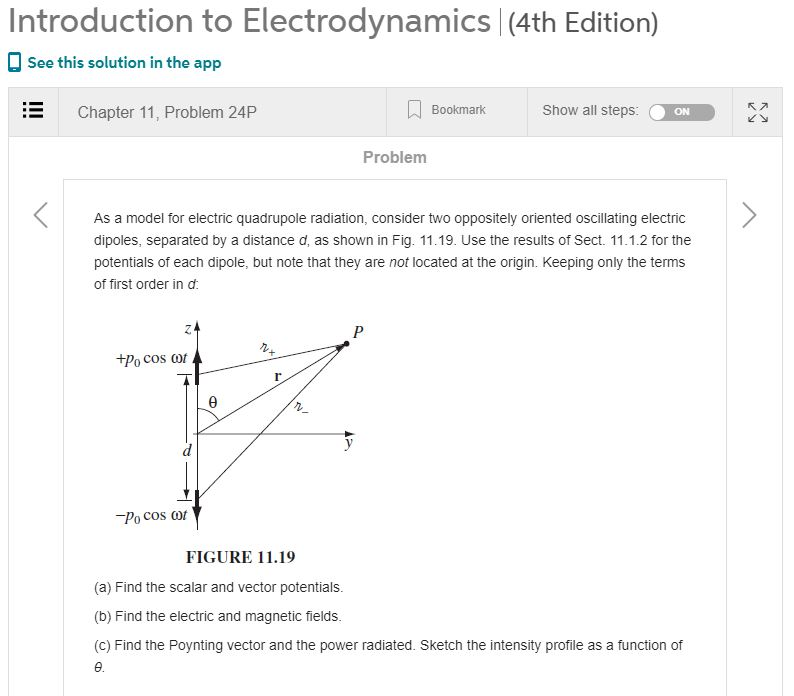
Prob. 3 (20 pts) Suppose that sources are harmonically oscillating as follows: p(r,t)=P(r)e and J(r,t)=J.(r)ei. In that case, the retarded vector potential A(r, t) could be expanded as Ar,t) = A + A 44,(1 - ikr)er 8r2 = A + A + A + [C-r'))g + car Jr')dr md (Eq. 1) mnd In this Prob. 3, we're going to show that the third term in (Eq. 1) corresponds to the vector potential for electric quadrupole radiation, i.e., Acq. 3-1 (5 pts): Show the relation below: (f:r')J, +(:J,)r' = {[(fr')J,1.V"}r' + r'{V":[(r')J.]} - r'fir'(V'.J.), where Jo = Jo(r'). 3-2 (5 pts): Using the result of (3-1) above, show A (r,t)=- 14,0)(1-ikr)e(a) 87r? [[r'cr-r')ps(r)]de". 3-3 (5 pts): Show that without affecting the B field, Acq can be written as A, (r,t)=- 14,0(1-ikr)ek-w) 24r? [[Br(r')=="flp.(r)dr'. 3-4 (5 pts): When a vector Q is defined as Q=[[3r'(^_r")=="f]ps(r")de", show the relation below: 19a (B = x,y,z), a=xy. where r = l+1,9+1.2=sin 0 cos p + sin & sin y + cos and Qaff is the electric quadrupole moment tensor, i.e., Que = [[Brar; (r")*8.p]ps(r)dt'. -Qelbo Qe-ow) Conclusion: We have obtained the vector potential for electric quadrupole radiation as follows: A (r,t)=- 14.0(1 - ikr) 4.cok 241r? 24tr Therefore, we can obtain the electromagnetic fields, generated by the oscillating electric quadrupole, using the followings: B. (r,t)= VA (r,t), B_(r,t) = -rxE_ (r,t). Prob. 4 (20 pts): By using the result of Prob. 3, solve Problem 24 in Chap. 10 (Radiation) of the textbook. [If you don't use the result of Prob. 3, you won't get any score.] d & +), *Note: Neglect the scalar potential, and then consider only the vector potential. d E *Hint: Suppose that four charges are located at (0, 0, +), (0, 0, ), (0, 0, 2 2 2 2 d & and (0, 0, f), where d >> E. 2 2 Introduction to Electrodynamics |(4th Edition) See this solution in the app Chapter 11, Problem 24P Bookmark Show all steps: ON R2 Ky Problem As a model for electric quadrupole radiation, consider two oppositely oriented oscillating electric dipoles, separated by a distance d, as shown in Fig. 11.19. Use the results of Sect. 11.1.2 for the potentials of each dipole, but note that they are not located at the origin. Keeping only the terms of first order in d. P 24 +Po cost 7 r n -Po cost FIGURE 11.19 (a) Find the scalar and vector potentials. (b) Find the electric and magnetic fields. (C) Find the Poynting vector and the power radiated. Sketch the intensity profile as a function of . Prob. 3 (20 pts) Suppose that sources are harmonically oscillating as follows: p(r,t)=P(r)e and J(r,t)=J.(r)ei. In that case, the retarded vector potential A(r, t) could be expanded as Ar,t) = A + A 44,(1 - ikr)er 8r2 = A + A + A + [C-r'))g + car Jr')dr md (Eq. 1) mnd In this Prob. 3, we're going to show that the third term in (Eq. 1) corresponds to the vector potential for electric quadrupole radiation, i.e., Acq. 3-1 (5 pts): Show the relation below: (f:r')J, +(:J,)r' = {[(fr')J,1.V"}r' + r'{V":[(r')J.]} - r'fir'(V'.J.), where Jo = Jo(r'). 3-2 (5 pts): Using the result of (3-1) above, show A (r,t)=- 14,0)(1-ikr)e(a) 87r? [[r'cr-r')ps(r)]de". 3-3 (5 pts): Show that without affecting the B field, Acq can be written as A, (r,t)=- 14,0(1-ikr)ek-w) 24r? [[Br(r')=="flp.(r)dr'. 3-4 (5 pts): When a vector Q is defined as Q=[[3r'(^_r")=="f]ps(r")de", show the relation below: 19a (B = x,y,z), a=xy. where r = l+1,9+1.2=sin 0 cos p + sin & sin y + cos and Qaff is the electric quadrupole moment tensor, i.e., Que = [[Brar; (r")*8.p]ps(r)dt'. -Qelbo Qe-ow) Conclusion: We have obtained the vector potential for electric quadrupole radiation as follows: A (r,t)=- 14.0(1 - ikr) 4.cok 241r? 24tr Therefore, we can obtain the electromagnetic fields, generated by the oscillating electric quadrupole, using the followings: B. (r,t)= VA (r,t), B_(r,t) = -rxE_ (r,t). Prob. 4 (20 pts): By using the result of Prob. 3, solve Problem 24 in Chap. 10 (Radiation) of the textbook. [If you don't use the result of Prob. 3, you won't get any score.] d & +), *Note: Neglect the scalar potential, and then consider only the vector potential. d E *Hint: Suppose that four charges are located at (0, 0, +), (0, 0, ), (0, 0, 2 2 2 2 d & and (0, 0, f), where d >> E. 2 2 Introduction to Electrodynamics |(4th Edition) See this solution in the app Chapter 11, Problem 24P Bookmark Show all steps: ON R2 Ky Problem As a model for electric quadrupole radiation, consider two oppositely oriented oscillating electric dipoles, separated by a distance d, as shown in Fig. 11.19. Use the results of Sect. 11.1.2 for the potentials of each dipole, but note that they are not located at the origin. Keeping only the terms of first order in d. P 24 +Po cost 7 r n -Po cost FIGURE 11.19 (a) Find the scalar and vector potentials. (b) Find the electric and magnetic fields. (C) Find the Poynting vector and the power radiated. Sketch the intensity profile as a function of