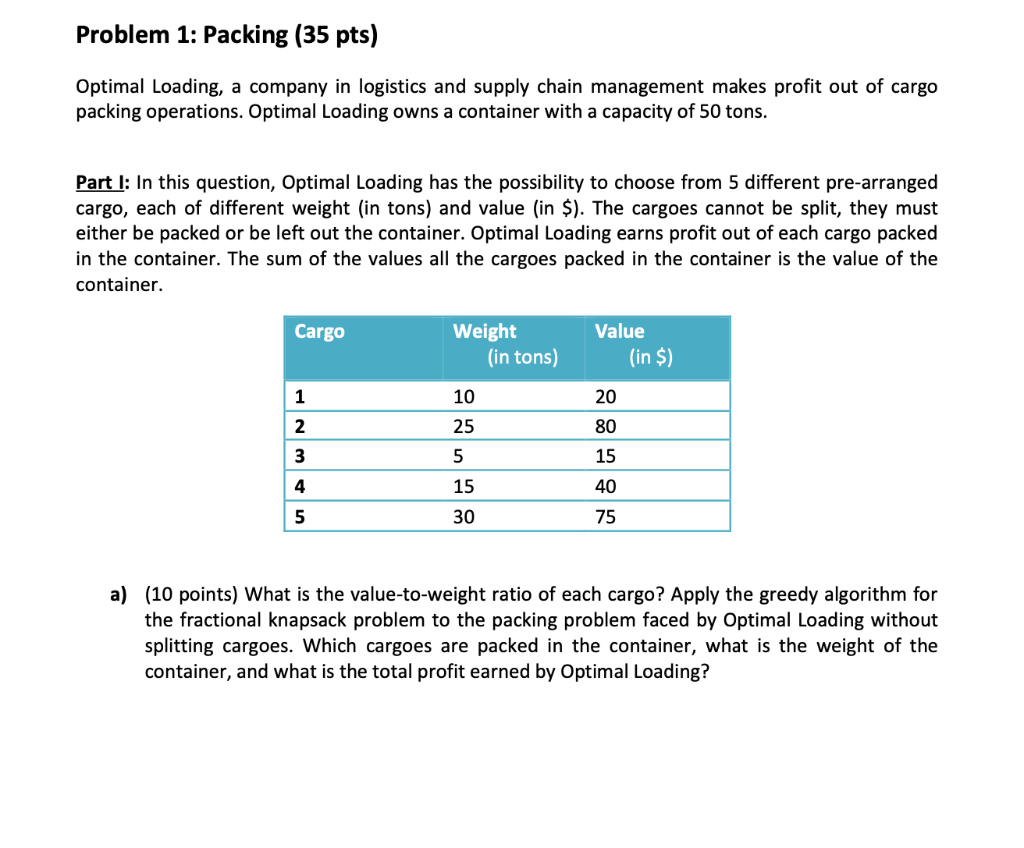


Problem 1: Packing (35 pts) Optimal Loading, a company in logistics and supply chain management makes profit out of cargo packing operations. Optimal Loading owns a container with a capacity of 50 tons. Part 1: In this question, Optimal Loading has the possibility to choose from 5 different pre-arranged cargo, each of different weight (in tons) and value (in $). The cargoes cannot be split, they must either be packed or be left out the container. Optimal Loading earns profit out of each cargo packed in the container. The sum of the values all the cargoes packed in the container is the value of the container. Cargo Value Weight (in tons) (in $) 1 10 20 2 25 80 3 5 15 4 15 40 5 30 75 a) (10 points) What is the value-to-weight ratio of each cargo? Apply the greedy algorithm for the fractional knapsack problem to the packing problem faced by Optimal Loading without splitting cargoes. Which cargoes are packed in the container, what is the weight of the container, and what is the total profit earned by Optimal Loading? b) (10 points) Solve the packing problem of Optimal Loading using Dynamic Programming. Divide the weights of cargoes by their greatest common denominator to reduce the number of operations, and report the table used for the calculations of the algorithm. What is the optimal value of the container? Which cargoes should be packed to achieve this optimal value? c) (5 points) is the solution found at Question a) optimal? Justify your answer. Part II: The greedy algorithm is very to use compared to the dynamic programming algorithm. This can be useful when decisions have to be made in the field in real-time. Hence, Optimal Loading is now trying to reverse engineer the problem and find situations where the greedy algorithm is optimal. d) (10 points) Assuming the capacity of the container remains 50 tons, construct an instance of the binary knapsack problem with 3 items named A, B and C, such that the sum of weights of the items is strictly greater than 50 tons and for which the greedy algorithm is optimal. Justify your answer. Report the weights, the value and the value to weight ratio of each item. Report the solution obtained by applying the greedy algorithm to this instance and discuss why this solution is optimal. Problem 1: Packing (35 pts) Optimal Loading, a company in logistics and supply chain management makes profit out of cargo packing operations. Optimal Loading owns a container with a capacity of 50 tons. Part 1: In this question, Optimal Loading has the possibility to choose from 5 different pre-arranged cargo, each of different weight (in tons) and value (in $). The cargoes cannot be split, they must either be packed or be left out the container. Optimal Loading earns profit out of each cargo packed in the container. The sum of the values all the cargoes packed in the container is the value of the container. Cargo Value Weight (in tons) (in $) 1 10 20 2 25 80 3 5 15 4 15 40 5 30 75 a) (10 points) What is the value-to-weight ratio of each cargo? Apply the greedy algorithm for the fractional knapsack problem to the packing problem faced by Optimal Loading without splitting cargoes. Which cargoes are packed in the container, what is the weight of the container, and what is the total profit earned by Optimal Loading? b) (10 points) Solve the packing problem of Optimal Loading using Dynamic Programming. Divide the weights of cargoes by their greatest common denominator to reduce the number of operations, and report the table used for the calculations of the algorithm. What is the optimal value of the container? Which cargoes should be packed to achieve this optimal value? c) (5 points) is the solution found at Question a) optimal? Justify your answer. Part II: The greedy algorithm is very to use compared to the dynamic programming algorithm. This can be useful when decisions have to be made in the field in real-time. Hence, Optimal Loading is now trying to reverse engineer the problem and find situations where the greedy algorithm is optimal. d) (10 points) Assuming the capacity of the container remains 50 tons, construct an instance of the binary knapsack problem with 3 items named A, B and C, such that the sum of weights of the items is strictly greater than 50 tons and for which the greedy algorithm is optimal. Justify your answer. Report the weights, the value and the value to weight ratio of each item. Report the solution obtained by applying the greedy algorithm to this instance and discuss why this solution is optimal









