Problem:

One way to define a balanced sequence of parentheses is as a string over the alphabet S={(,)} such that: its total number of characters equals its total number of characters; and in each of its prefixes, there are at least as many characters as there are ) characters.

The debt of a prefix of a balanced sequence of parentheses is the number of (characters in the prefix minus the number of characters in it. The depth of a balanced sequence of parentheses is the maximum debt among all its prefixes.

For a given d N we can define the language P_d of all balanced sequences of parentheses having depth at most d. We can also define the language

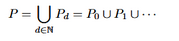
of all balanced sequences of parentheses.

Later in the course we shall see that P is not a regular language. This will be shown in a systematic manner, but it is possible to prove this fact using only material covered in class. For now this is left as a challenging exercise but is not part of the assignment.

In this problem you must answer the following question and prove that your answer is correct. Which values of d N are such that P_d is a regular language?