Prove or disprove each of the following statements, where in each case G=(V; E) is a connected undirected weighted graph with n vertices and m edges.

(a)If G has 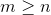edges and a unique heaviest edge e, then e is not part of any minimum spanning tree of G.

(b)If G has 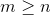edges and a unique lightest edge e, then e is part of every minimum spanning tree of G.

(c)If e is a maximal weight edge of a cycle of G, then there is a minimum spanning tree of G that does not include e.

(d)Prim's algorithm returns a minimum spanning tree of G even when the edge weights can be either positive or negative

mn mn