public class Geometry { // Test to see if two double-precision floating-point // values are "equal." The values are considered // equal when their difference is small. public static boolean floatEquals(double a, double b) { return false; // Replace with your code }

public static double distance(double x1, double y1, double x2, double y2) { return 0.0; // Replace with your code }

public static double slope(double x1, double y1, double x2, double y2) { return 0.0; // Replace with your code }

public static double intercept(double x1, double y1, double x2, double y2) { return 0.0; // Replace with your code }

public static String lineToString(double m, double b) { return "Line equation"; // Replace with your code }

public static String lineToString(double x1, double y1, double x2, double y2) { return lineToString(slope(x1, y1, x2, y2), intercept(x1, y1, x2, y2)); }

}

import java.util.Scanner;

public class TestGeometry {

private static void doDistance(double x1, double y1, double x2, double y2) { System.out.print("The distance between (" + x1 + ", " + y1 + ") and "); System.out.println("(" + x2 + ", " + y2 + ") is " + Geometry.distance(x1, y1, x2, y2)); }

private static void doSlope(double x1, double y1, double x2, double y2) { double slope = Geometry.slope(x1, y1, x2, y2); String slopeString; if (slope == Double.POSITIVE_INFINITY) { slopeString = "undefined"; } else { slopeString = Double.toString(slope); } System.out.print("The slope of the line between (" + x1 + ", " + y1 + ") and "); System.out.println("(" + x2 + ", " + y2 + ") is " + slopeString); }

private static void doIntercept(double x1, double y1, double x2, double y2) { if (Geometry.slope(x1, y1, x2, y2) == Double.POSITIVE_INFINITY) { System.out.print("The x-"); } else { System.out.print("The y-"); } System.out.print("intercept of the line between (" + x1 + ", " + y1 + ") and "); System.out.println("(" + x2 + ", " + y2 + ") is " + Geometry.intercept(x1, y1, x2, y2)); }

private static void doEquation(double x1, double y1, double x2, double y2) { System.out.print("The equation of the line between (" + x1 + ", " + y1 + ") and "); System.out.println("(" + x2 + ", " + y2 + ") is " + Geometry.lineToString(Geometry.slope(x1, y1, x2, y2), Geometry.intercept(x1, y1, x2, y2))); }

public static void main(String[] args) { Scanner scan = new Scanner(System.in); do { double p_x1, p_y1, p_x2, p_y2;

// Get the points from the user System.out.print("Enter the point coordinates x1, y1, x2, y2: "); p_x1 = scan.nextDouble(); p_y1 = scan.nextDouble(); p_x2 = scan.nextDouble(); p_y2 = scan.nextDouble();

// Exercise the geometry methods doDistance(p_x1, p_y1, p_x2, p_y2); doSlope(p_x1, p_y1, p_x2, p_y2); doIntercept(p_x1, p_y1, p_x2, p_y2); doEquation(p_x1, p_y1, p_x2, p_y2); System.out.println("----------------------"); } while (true); // scan.close(); } }

Please help with Java Program!

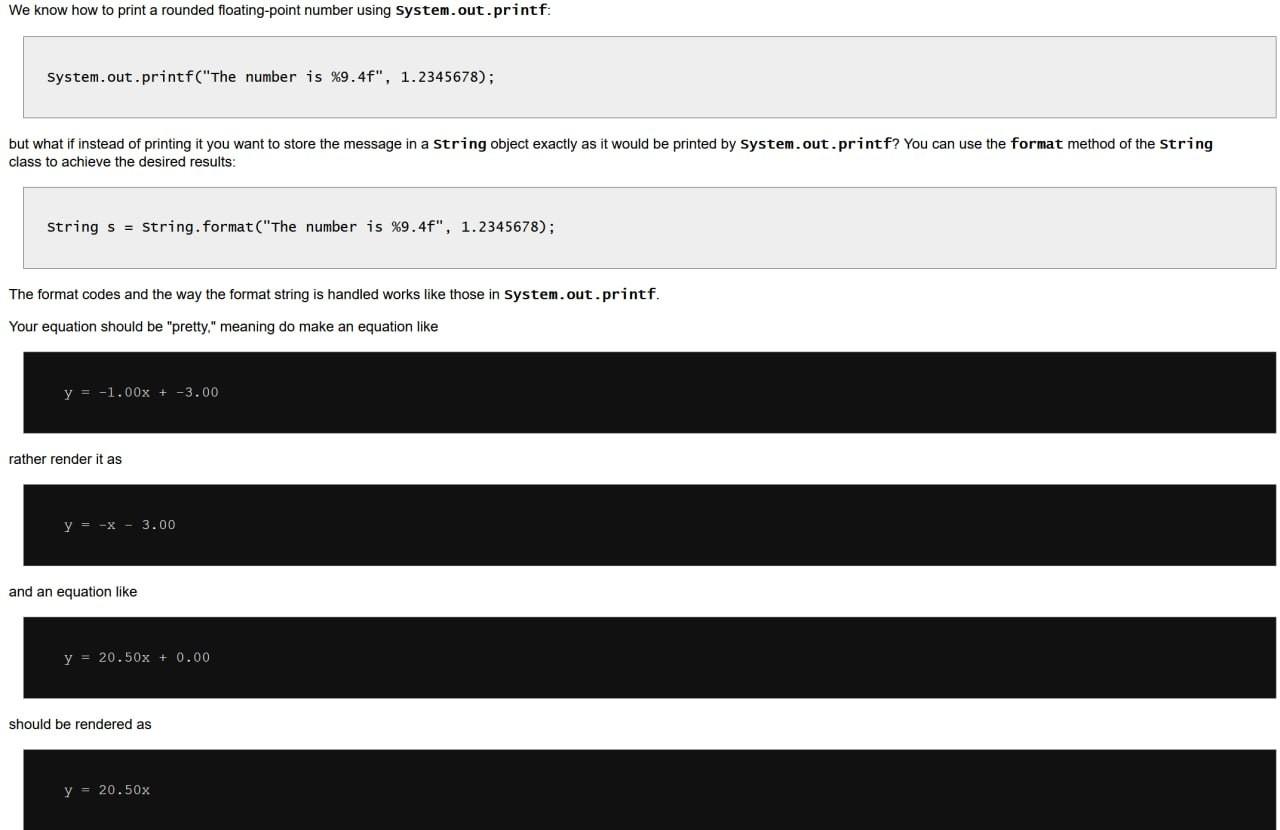
In this assignment you will work with two Java source files: - Geometry_ java. This file contains the Geometry class definition. Within this class you will implement five class methods. - TestGeometry. java. This program uses the methods within the Geometry class, allowing a user to enter in the coordinates of two geometric points. The program then prints four things: 1. the distance between the two points, 2. the slope of the line that passes through the two points, 3. the y-intercept of the line that passes through the two points, unless the line is vertical; in which case the program prints the x-intercept of the line, and 4. the equation of the line (in slope-intercept form) that passes through the two points. You should not modify the code in TestGeometry. java. Your task is to implement the methods in Geometry. java. The code within TestGeometry. java will use this functionality. The program found in TestGeometry. java will compile and run with the provided skeletal Geometry. java file, but the TestGeometry. java program will not produce the correct results until you correctly implement the expected methods in Geometry. java. The required methods are: floatEquals Remember that many floating-point numbers do not have an exact representation. This means the == operator may consider two floating-point numbers unequal even though we believe they should be equal. Complete the floatEqua 7 s method that returns true if its two double-precision floating-point arguments are within 0.0001 of each other; otherwise, the method should return fa7se. distance The distance between two points (x1,y1) and (x2,y2), is given in the following formula: (x2x1)2+(y2y1)2 Complete the method named distance that accepts four double-precision floating-point arguments x1,y1,x2, and y2, in that order, representing two geometric points ( x1,y1), and (x2,y2). It m=x2x1y2y1 Complete the method named slope that accepts four double-precision floating-point arguments and returns the double-precision floating-point value representing the slope of the line passing through the two points represented by the arguments. Watch out for vertical lines! Return the predefined constant Double. POSITIVE_INFINITY to represent infinity if the line is vertical. Note: The method should throw an I11ega1ArgumentException if the caller passes parameters that represent two equal points. The following statement achieves the desired behavior: throw new I7legalargumentexception() intercept An intercept is a number that represents a location on an axis where a line intersects that axis. The y-intercept of a line is the y value of the point where a line crosses the y-axis. Complete the method named intercept that accepts four double-precision floating-point arguments representing the coordinates of two points. The method ordinarily returns the double-precision floatingpoint value representing the y-intercept of the line that that passes through the two points defined by the arguments. For non-vertical lines, we can compute the y-intercept from the y=mx+b form of a line. Solving for b, we get b=ymx : b=ymx This means if we know the slope, m, we can plug in the (x,y) coordinates from either point to compute b. Vertical lines do not have a y-intercept, so the intercept method instead should return the x-intercept for vertical lines. If the two points form a vertical line, it is easy to determine the x-intercept. Note: The method should throw an I11ega1ArgumentException if the caller passes parameters that represent two equal points. line ToString The equation of a line in slope-intercept form is y=mx+b System.out.printf("The number is %9.4f,1.2345678 ) but what if instead of printing it you want to store the message in a String object exactly as it would be printed by System.out.printf? You can use the format method of the String class to achieve the desired results: String s= string. format ("The number is %9.4f,1.2345678 ); The format codes and the way the format string is handled works like those in system.out.printf. Your equation should be "pretty," meaning do make an equation like y=1.00x+3.00 rather render it as y=x3.00 and an equation like y=20.50x+0.00 should be rendered as y=20.50x method to fine tune the exact output. A vertical line has the form where b is the x-intercept. Your method should return a string that correctly represents the equation for vertical lines. the representation more attractive. If you do not have the time or interest to make the string "pretty," you may elect to receive 9/10 points for the assignment if your string is just mathematically correct. 2. Organization Copy the files 5echetry. Java and Testgeonetry. Java to a new project. Do not change the names of the files. Your task is to complete the methods in Geometry. java. Do not touch any of the code in the TestGeonetry. java file. within the Testgeometry class. produced by this method to two decimal places. 3. Strategy under those restricted conditions, then add vertical line capability and afterwards, if time permits, pretty output. Check out keyboardl