Python 3

You will need the following instance attributes:

front - index of the front of the queue

rear - index of the first empty slot (or index of the last element, it is up to you)

num_elems - integer that tracks the number of elements present in the queue

capacity - capacity of the queue, initially 5, initialize your array with elements set to None

data - an array of length capacity (represents your queue)

To implement the behavior of the ADT you need to provide implementations for the following methods:

dequeue - removes and returns the front element

enqueue - adds element, doubling the capacity if is full

is_full - checks whether a queue is full. Returns True if full, False otherwise.

is_empty - checks whether a queue is empty. Returns True if empty, False otherwise.

print_queue - prints queue.

Format: Assume that elements 4, 5, 6, 7, 8 were added to the queue q. Then q.print_queue() will print: [ | 4 | 5 | 6 | 7 | 8 | ]

If a queue is empty, print: [ ] TESTING:

This question is designed to test your queue, so make sure that you debug it thoroughly. If something is not implemented correctly, then the points for this problem might be lost.

For this problem, you will be implementing a method called cursed_carousel that simulates a cursed carousel using the queue from question 4.1. This function should take in 2 positive integers, n and m.

n will indicate the number of passengers on the carousel, while m indicates the kicking off factor. After the carousel starts, it acts as a queue, where the n people are numbered 1 through n and were inserted in order

[1, 2, 3, ... , n]. It then goes through the queue, only kicking off a passenger every mth time, while adding the removed people to the end of the queue.

Thus, after 1 iteration of that, the queue will look like [4 ,5, 6, ... ,n, 1, 2], while 3 has been removed and 1 and 2 were added to the end. We want you to have a function that simulates this curse and prints out the ejected rider's number until everyone has been kicked off of the carousel.

Example:

cursed_carousel(6,3)

Start with [1, 2, 3, 4, 5, 6]

Move 1 and 2 to the end, print 3.

Now we have [4, 5, 6, 1, 2]

Move 4 and 5 to the end, print 6.

Now we have [1, 2, 4, 5]

Move 1 and 2 to the end, print 4.

Now we have [5, 1, 2]

Move 5 and 1 to the end, print 2.

Now we have [5, 1]

Move 5 and 1 to the end, now 5 is at the front again, so print 5.

Now we have [1]

Move 1 to the end twice, print 1.

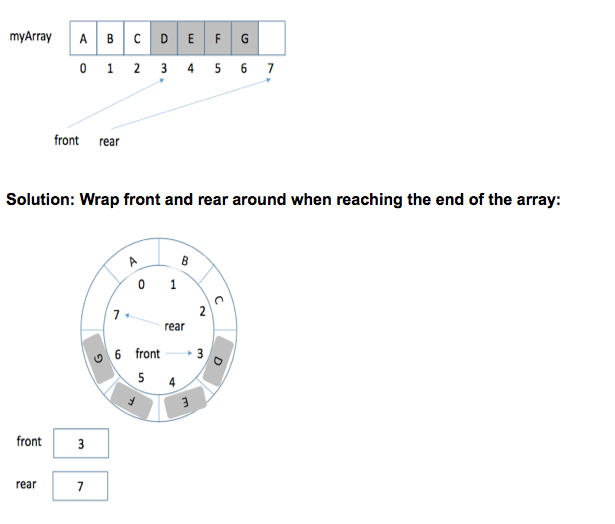
Define class Queue that implements the ADT (Abstract Data Type) Queue using a circular array. . You must use a np.array for this question: o Somewhere in your constructor you must have a line that looks like self.data-np.array..... . . . . You must observe the FIFO convention. When implementing a queue, we have to worry about running time for its basic operations: dequeue and enqueue. Both of them must run in Theta Unfortunately, a regular array does not give you desired complexity. Let me explain why: We will assume that front (index) points to the front of a queue, and rear (index) points to the end of a queue, to the next available location front rear Front always stays at 0, and we move rear when we add elements. Issue1: Each time when we delete an element from front, we have shift everything to the left: Theta (n) rear front 0 Rear always stays at 0, and we move front when we remove elements. Issue2: Each time we add an element to rear, we have shift everything to the right: Theta(n) front rear Now we move both front and rear to the right when we add/remove an element. This will ensure that the running time is Theta(1) Issue3: Space. Each time we move front and rear to the right, space on the left is not used anymore (Never can get to indices 0, 1, 2) Define class Queue that implements the ADT (Abstract Data Type) Queue using a circular array. . You must use a np.array for this question: o Somewhere in your constructor you must have a line that looks like self.data-np.array..... . . . . You must observe the FIFO convention. When implementing a queue, we have to worry about running time for its basic operations: dequeue and enqueue. Both of them must run in Theta Unfortunately, a regular array does not give you desired complexity. Let me explain why: We will assume that front (index) points to the front of a queue, and rear (index) points to the end of a queue, to the next available location front rear Front always stays at 0, and we move rear when we add elements. Issue1: Each time when we delete an element from front, we have shift everything to the left: Theta (n) rear front 0 Rear always stays at 0, and we move front when we remove elements. Issue2: Each time we add an element to rear, we have shift everything to the right: Theta(n) front rear Now we move both front and rear to the right when we add/remove an element. This will ensure that the running time is Theta(1) Issue3: Space. Each time we move front and rear to the right, space on the left is not used anymore (Never can get to indices 0, 1, 2)