[PYTHON in Jupyter notebook]

Question 1 is done (I think correctly). I am confused on how to do question 2.

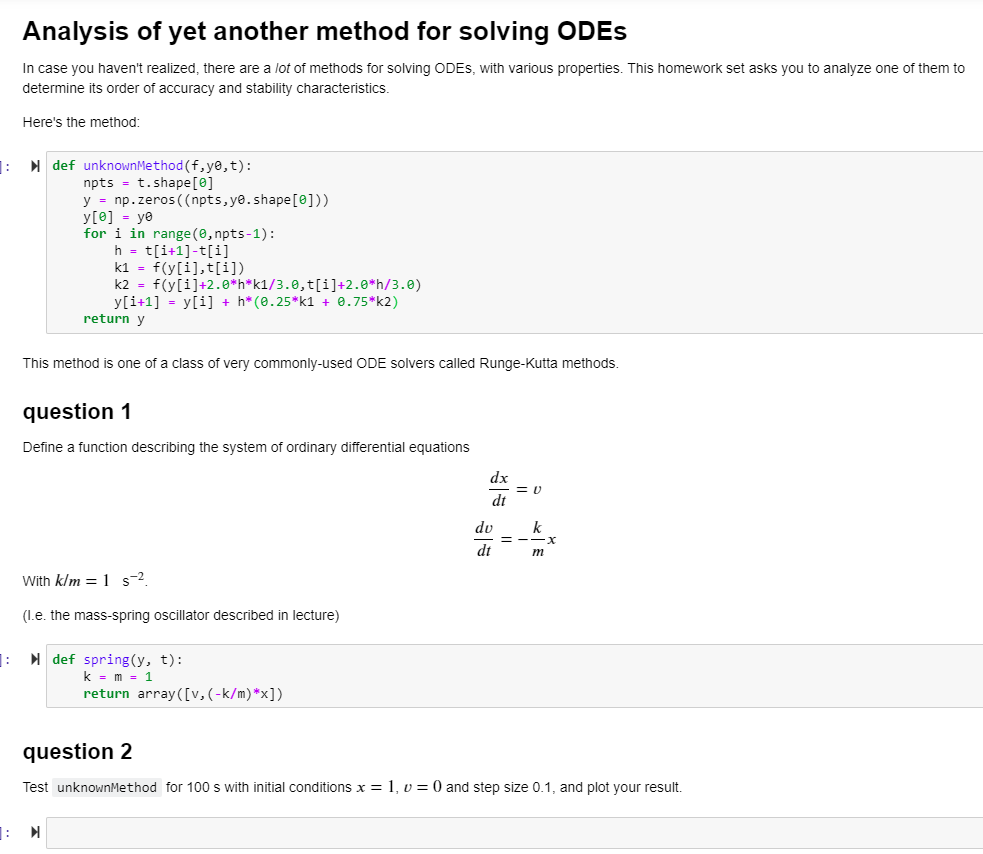
Analysis of yet another method for solving ODES In case you haven't realized, there are a lot of methods for solving ODES, with various properties. This homework set asks you to analyze one of them to determine its order of accuracy and stability characteristics. Here's the method: |: def unknownMethod(f,ye,t): npts = t.shape[@] y = np.zeros((npts,ye.shape[@])) y[@] = ye for i in range (, npts-1): h = t[i+1]-t[i] k1 = f(y[i],t[i]) k2 = f(y[i]+2.0*h*k1/3.0,t[i]+2.0*h/3.0) y[i+1] = y[i] + h*(0.25*k1 + 0.75*K2) return y This method is one of a class of very commonly-used ODE solvers called Runge-Kutta methods. question 1 Define a function describing the system of ordinary differential equations dx dt =U du dt k =-=X With klm = 1 s-2 (I.e. the mass-spring oscillator described in lecture) 1: def spring(y, t): k = m = 1 return array([v,(-k/m)*x]) question 2 Test unknownMethod for 100 s with initial conditions x = 1, v= 0 and step size 0.1, and plot your result. 1