python

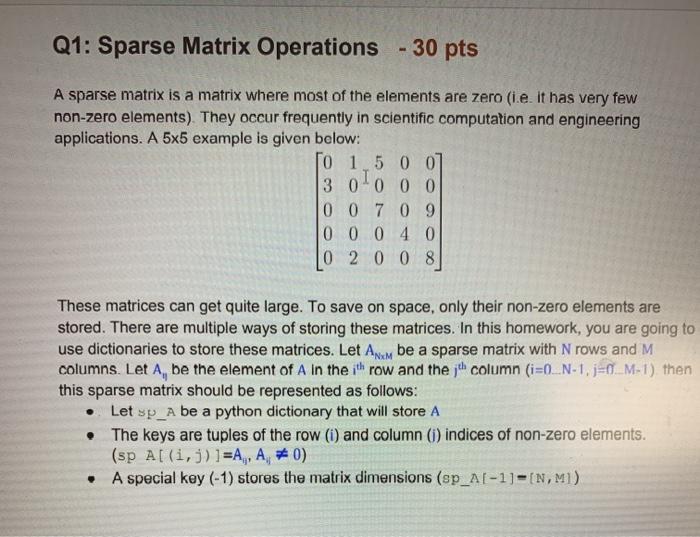
Q1: Sparse Matrix Operations - 30 pts A sparse matrix is a matrix where most of the elements are zero (ie. It has very few non-zero elements) They occur frequently in scientific computation and engineering applications. A 5x5 example is given below: To 1.5 0 0] T 3 0 0 0 0 0 0 7 0 9 0 0 0 4 0 0 2 0 0 8 These matrices can get quite large. To save on space, only their non-zero elements are stored. There are multiple ways of storing these matrices. In this homework, you are going to use dictionaries to store these matrices. Let Anm be a sparse matrix with N rows and M columns. Let A, be the element of A in the ith row and the j column (i=0_N-1.j=0. M-1) then this sparse matrix should be represented as follows: . Let sp_A be a python dictionary that will store A The keys are tuples of the row (i) and column (i) indices of non-zero elements. (sp A (1,3)]=A,, A, 0) A special key (-1) stores the matrix dimensions (sp_AC-1]=[N,M1) The starter code for this question is given to you in sparse_matrices.py. This question has three parts: Part 1: You will be given the matrices in a list of lists format. You need to convert them to the aforementioned sparse representation. Fill in the dense_to_sparse function to complete this part A TO 3 0 0 0 sp_A[(0,1)) = 3, sp_A|(1,0)) = 1, sp_A(-1) = (2,3) Part 2: You are going to implement the matrix transpose operation (switching the row and column indices of non-zero elements, A -A) for the dictionary based sparse matrix representation described in this question. Fill in the sparse_transpose function to complete this part To 1 307 A= AT = 30 1 0 0 LO 0 -6 Part 3: The code for matrix multiplication for list of lists implementation is given to you. You are going to implement matrix multiplication for the dictionary based sparse matrix representation described in this question. Fill in the sparse_mat_mult function to complete this part. Let AN. M. BMxk, be two matrices and CNak AB their multiplication. The elements of C are calculated as: = C) = 2A, Bk For all of the parts, follow the comments. Do not iterate over the entire rows and columns for any of the parts! This will be inefficient and you will lose points. There is an example