python question 2

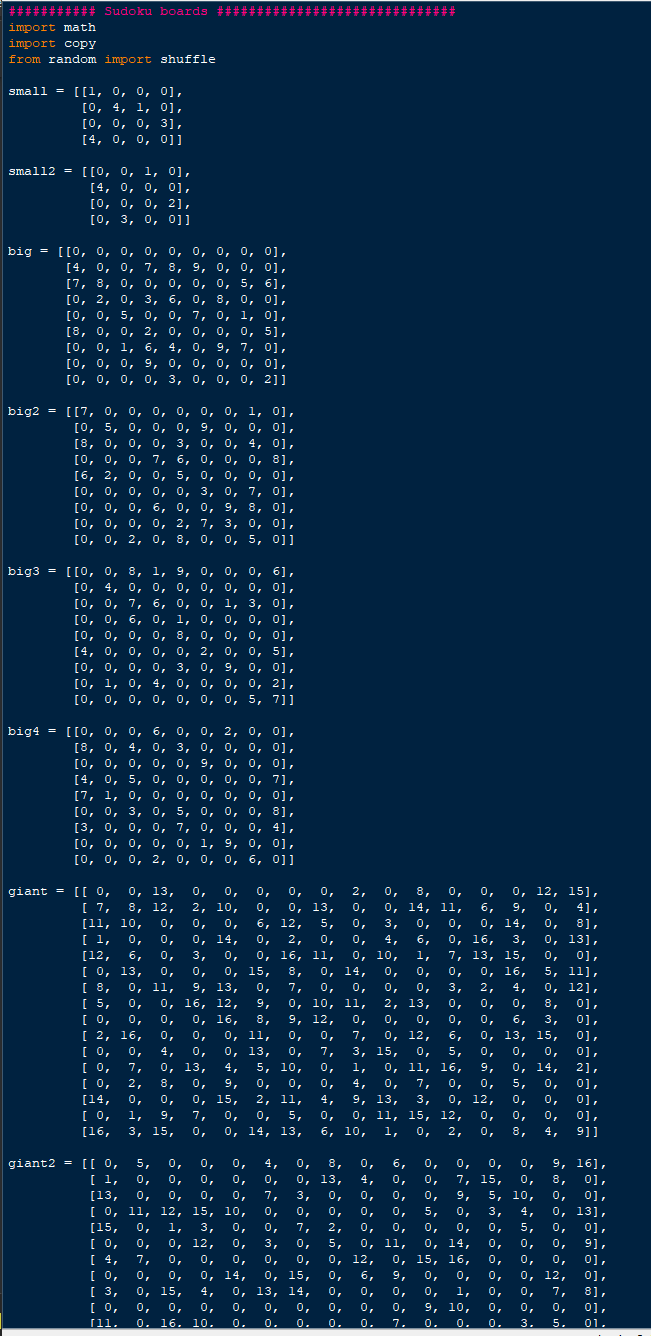
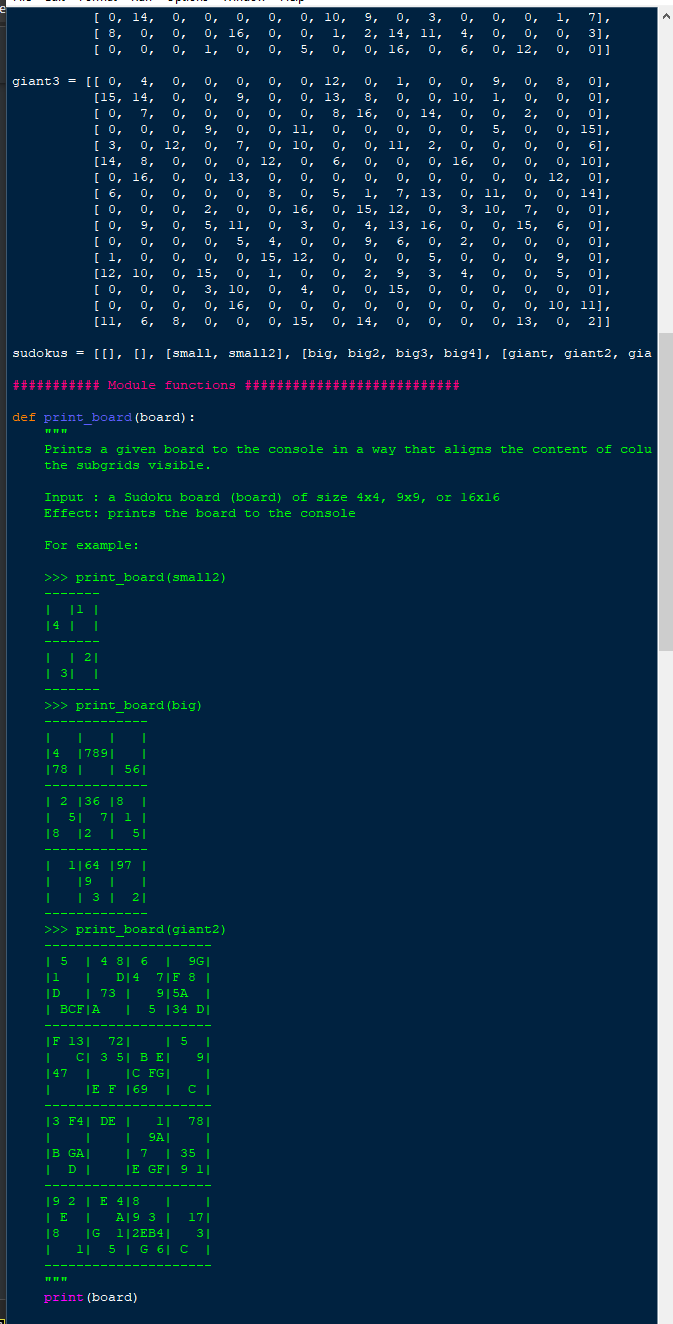
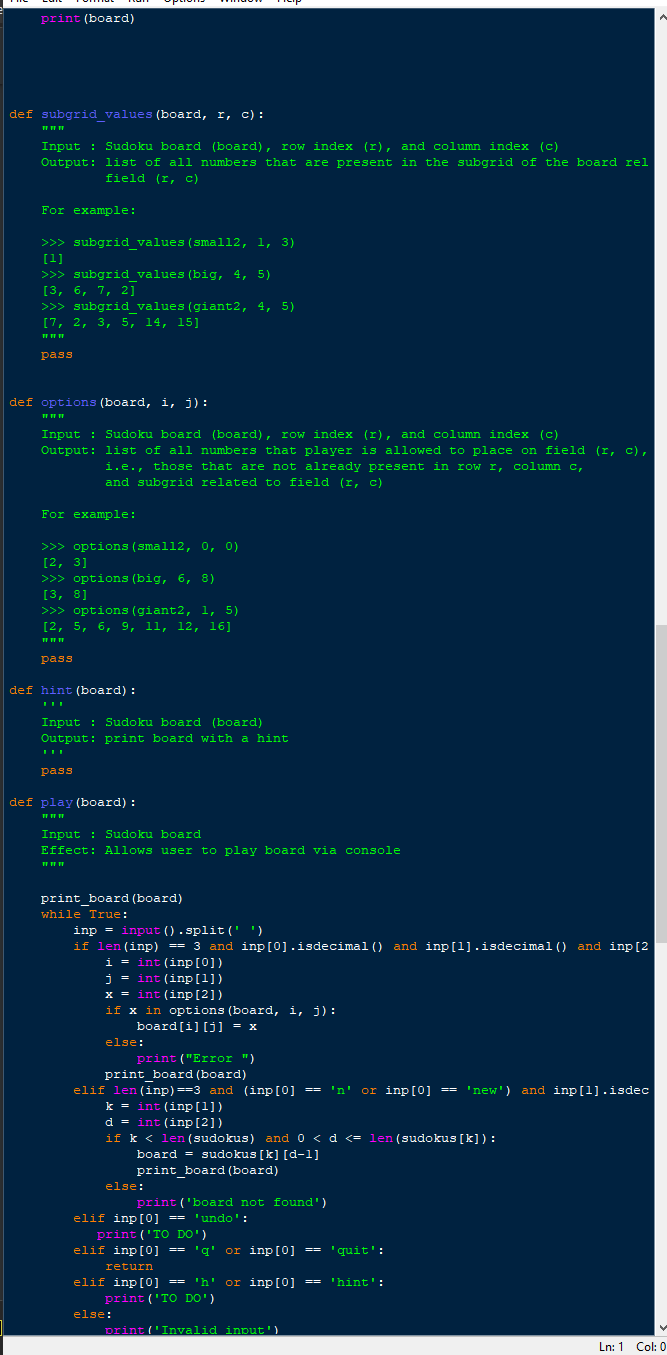
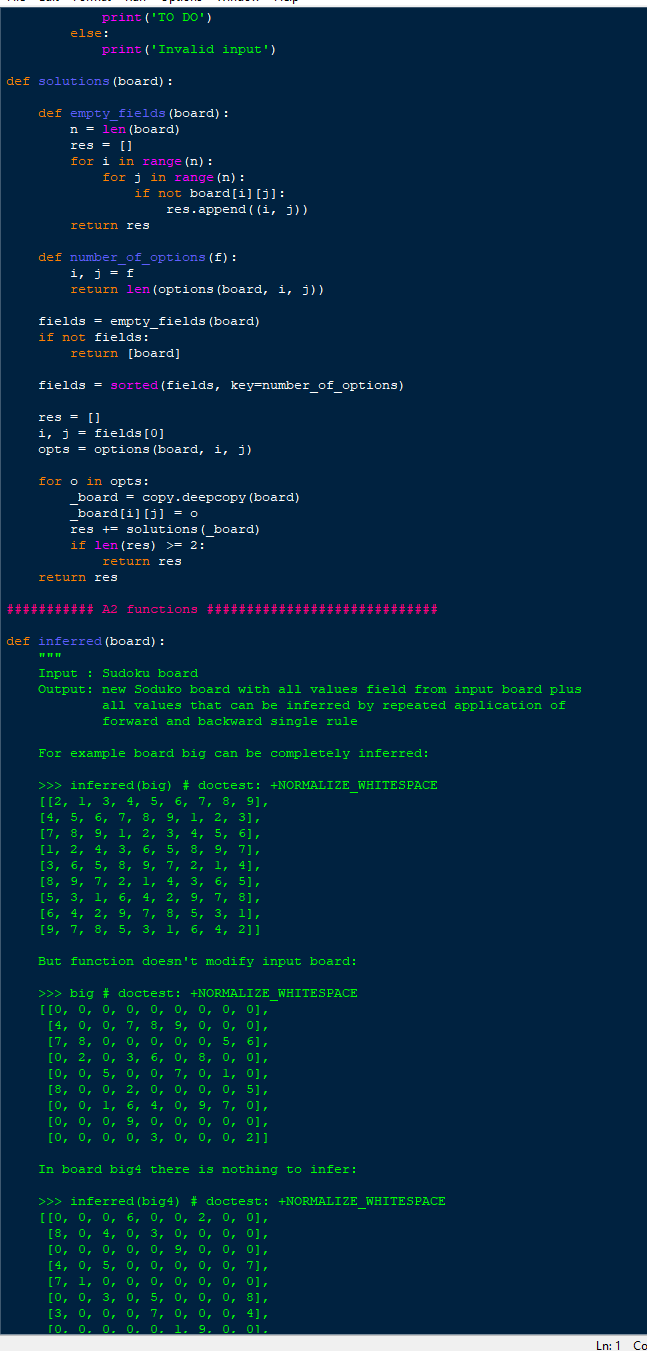
Task 2: Generting Suduko board In the template file, we provided solutions function, this function will return possible solutions to the board as a list of solutions, where each item in this list is a solved board. You don't need to understand how this function works. However, you just need to understand the format of its input and output as you will use this function to extend the behaviour of the play function such that on input 'g' k, (i.e., the letter g followed by an integer k> 1), or 'generate' k, it generates a new random kby k? Sudoku board such that the board has a unique solution. Hints: Think of a good decomposition of this problem. Some ideas for useful subproblems are, e.g., generating a random full game board that is valid (i.e., satisfies the placement constraints of Sudoku) and checking whether a given partially filled board has a unique solution. The partially filled board can be generated by repeatedly removing a number from the board (set that cell to 0) and see if the resulting game board would still have a unique solution. The number to be removed can be selected randomly. You should aim to remove as much numbers as possible. For randomising you can use the function shuffle from the random module. Your initial solutions to this problem are likely rather slow. Make sure to first test with the smallest board size (k =2). 4 ########### Sudoku boards ###### import math import copy from random import shuffle small = [[i, 0, 0, 0], [0, 4, 1, 0], [0, 0, 0, 3], [4, 0, 0, 0]] small2 = [[0, 0, 1, 0], [4, 0, 0, 0], [0, 0, 0, 2], [0, 3, 0, 0]] big = [[0, 0, 0, 0, 0, 0, 0, 0, 0], [4, 0, 0, 7, 8, 9, 0, 0, 0], ' [7, 8, 0, 0, 0, 0, 0, 5, 6], [0, 2, 0, 3, 6, 0, 8, 0, 0], ' ' [0, 0,5, 0, 0, 7, 0, 1, 0], [8, 0, 0, 2, 0, 0, 0, 0, 5], '' ' . [0, 0, 1, 6, 4, 0, 9, 7, 0], [0, 0, 0, 9, 0, 0, 0, 0, 0], 10, 0, 0, 0, 3, 0, 0, 0, 211 0, 3, 7, 0], 0, 7], big2 = [[7, 0, 0, 0, 0, 0, 0, 1, 0], [0, 5, 0, 0, 0, 9, 0, 0, 0], [8, 0, 0, 0, 3, 0, 0, 4, 0], [0, 0, 0, 7, 6, 0, 0, 0, 8], [6, 2, 0, 0, 5, 0, 0, o, 0], (0, 0, 0, 0, 9: 0, 7, [0, 0, 0,6, 0, 0, 9, 8, 0], [0, 0, 0, 0, 2, 7, 3, 0, 0], [0, 0, 2, 0, 8, 0, 0, 5, 0]] big3 = [[0, 0, 8, 1, 9, 0, 0, 1 o, 6], [0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 7, 6, 7,6, 0, 0, 1, 3, 0], [0, 0,6, 0, 1, 0, 0, 0, 0], 0 10, 0, 0, 0, 8, 0, 0, 0, 0], 0, , 0 [4, 0, 0, 0, 0, 2, 0, 0, 5], 000000 [0, 0, 0, 0, 3, 0, 9, 0 9, 0, 0], [0, 1, 0, 4, 0, 0, 0 o, o, 2], [0, 0, 0, 0, 0, 0, 0, 5, 7]] big4 = [[0, 0, 0, 6, 0, 0, 2, 2, 0, 0], [8, 0, 4, 0, 3, 0, 0, 0, 0], 3, [0, 0, 0, 0, 0, 9, 0, 0, 0], 00 [4, 0,5, 0, 0, 0, 0, 0, [7, 1, 0, 0, 0, 0, 0, 0, 0], 000000 [0, 0, 3, 0,5, 0, 0, 0, 8], 000 . [3, 0, 0, 0, 7, 0, 0, 0, 4], [0, 0, 0, 0, 0, 0, 1, 9, o, 0], [0, 0, 0, 2, 0, 0, 0, 6, 0]] 0, 13, 0, 0, 0, 0, 0, giant = [[ 0, 2 0, 12, 15) 0, 8, 0, [ 7, 8, 12, 2, 10, 0, 0, 13, 4], 0, 0, 14, 11, 6, 9, 0, [11, 10, 0, 0, 6, 12, 0, 5, 0, 3, 0, 14, 0, 0, 8), 0, 0, 14, 1, 0, 0, 0, 16, 3, 0, 13), [12, 0, 0, 0), 3, 0, 16, 11, 0, 10, 7, 13, 15, '' o 1 1 [ 0, 13, 0, 0, 0, 15, 8, 0, 14, 0, 0, 16, 5, 11], 0, 180 ' ' ' 9, 13, [ 8, 0, 11, , 7, 0, 0, 2, 4, 0, 12), in 1 12 10 ' ' ' ' 13. [ 5, 0, 0, 16, 12, 9, 0, 10, 11, 2, 13, 0), 0, 0, 8, '' 16' ' ' a 120 ' o [ 0, 0, 0, 16, 8, 0, 9, 12, , 0, 0], 0, 6, 3, ' ' ' ' 16 [ 2, 16, 0, 0, 0, 11, 0, 7, 0, 12, 0], 6, 0, 13, 15, 2. 13 '' [ 0, 0, 4, 0, 13, 0, 0, 3, 15, 0, 5, 0], 0, 0, 0, ' 13 a' ' ' [ 0, 7, 0, 13, 4, 5, 10, 0, 1, 2), 0, 11, 16, 9, 0, 14, [ 0, 2, 8, 9, 0, 0, 0, 0, 4, 0, 7, 0], 0, 0, 5, 0, ' ' (14, 0, 15, 0, 2, 11, 0, 4, 0, 12, 9, 13, 0, 0, 3, 0], [ 0, 1, 9, 7, 0, 0, 5, 0], 0, 0, 11, 15, 12, 0, 0, 0, [16, 0, 14, 13, 3, 15, 6, 10, 0, 1, 2, 0, 8, 4, 9]] 0, o, giant2 = [[ 0, 5, 8, 0, 9, 16), 0, [i, 0, 0, 0), 0, O, 0, 13, 8, 0, 7, 15, a [13, 0, 0, 9, 5, 10, 0, 0), 2 [ 0, 11, 12, 15, 0, 3, 4, 0, 13), (15, 0, 1, 3, 0, 0, 5, 0, 0], [0, 0, 12, 0, 11, 9], 0, 14, 0, 0, 0, [ 4, 0, 0, 0, 12, 0], 0, 15, 16, 0, 0, 0, [ 0, 0, 0, 0, 14, 0, 15, 9, 0, 0, 0, 0, 12, 0], 0, 13, 14, 0, 0, [ 3, 7, 8), 0, 15, 9, 10, [ 0, 0, o, o, 0], 01. rii. o. 16. 10. . 1, 0, 0, [ 0, 14, [ 8, 0, [ 0, 0, o, o, 0, 0, 0, 0, 16, i, 0 0, o, o, 0, 0, 10, o, , i, , 5, , o, , 9, o, 3 2, 14, 11, 0, 16, 0, 0, 4, 6, o, 0, 0, 0, 0, 12, i, 0 0, 7], 3], 0]] o, 0, 0 [ 0, 0 0, 0, 2, 0. 0, 0, . o 0. 0. 0, 16. [ 0, 16, 0, . giant 3 = [[ 0, 4, 4 0, o, o, o, 0, 12, 0, i, o, o, 9, 8, 0), [15, 14, o, 9 o, 0, 13, , , 8, , o, , 0, 10, i, 0, [ 0, 7, 7 o, o, o, o, o, , 8, 16, 0, 14, , 0, 0, 0, 0, 9, 0, 0, 11, , , 5, 12 0 0, 12, 0, 7 [ 3, 7 10 7, 0, 10, 0, , 0, 11, 11, 2, 0, 0, 0, 0, 6), 8 [14, 8, 0, 12, 0. o o O, 6, 0, 0, 0, 16, 0, 0 0, 10), o 18 0 0 0 0, 13, 0, 0, 0, 0, 0, 0, 0, , [ 6, 6 0 713 0 0 0, 0, 8, o, 5, 1 7, 13, 0, 11, 0, 16 10, [ 0, 15, 12, 0, 0, 0, 16, 2, 0, 0 3, 10, 7, O, 0], ' ' [ 0, 5 u 9, 5, 11, 0, , 3, 0, 3 4, 4, 13, 16, 0, 0, 15, 6, [ 0, 0 ' ' O, 0 5, 4, 0, 0, 6, 0, 9, 0 0 o [1, 5. 0, 0.15. 12. 0, 0, 15, 12, O, O, 0, 5, [12, 10, 0, 15, 0, , 1, 0, i o, 2, 9, 3, 0], [0, 0, o, 3, 10, o, 4, o, 0, 15, o, 0], o, o, 0, 16, o, o, o, o, 0, 10, 11], ] 6, 8, 0, 0, 0 0, 15, 0, 14, 0, o, 0, 0, 13, 0, 2]] , 0, 0, 0, 0, 0, 0, 0, o, ] 0), o, 0], 0, 15), 151. 0, 0, 12, 0], 01. 0, 141, 141. i 0], oi. oi. O, 0, 0), 0, oi. 9, 0), 5, ], 0, 0, 0, 6 0, 0, 5 2. 0, A 4, 0. 0, 0. , 0, 0, 0. 0, , , 0, 0, 0, [ 0, [ll, sudokus = [[], [], [small, small2], [big, big2, big3, big4], [giant, giant2, gia ########### Module functions ########################### def print board (board): Prints a given board to the console in a way that aligns the content of colu the subgrids visible. Input : a Sudoku board (board) of size 4x4, 9x9, or 16x16 Effect: prints the board to the console For example: >>> print_board (small2) | 1 | 14 | 21 | 31 >>> print_board (big) I 14 1789 178 | | 561 | 2 136 18 T | 51. 7|1| 711 18 12 15 51 I 1|64 197 | I 19. I I | 3 | 20 >>> print_board (giant2) | 5 | 4 8 6 1 9G| ji T D4 70F 8L ID | 73 | 9|5A | BCF|A T5 5 34 DI IF [F 131 72] | 5 | C] 3 5| BE| 91 147 | IC FG T 1 E F 169 1 C D CL 13 13 F4| DE | 1| 781 | T I I 9A| T |B GAI 17 | 35 | I DI LE GF 911 19 2 | E 48 2 | ET A93L 17| 18 IG 1|2EB4] | 31 I 11 5 | G 6| C | 1 TT TT TT print (board) print (board) def subgrid_values (board, I, c): Input : Sudoku board (board), row index (1), and column index (c) Output: list of all numbers that are present in the subgrid of the board rel field (r, c) For example: >>> subgrid_values (small2, 1, 3) [1] >>> subgrid_values (big, 4, 5) [3, 6, 7, 2] >>> subgrid_values (giant2, 4, 5) [7, 2, 3, 5, 14, 15] pass def options (board, i, j): Input : Sudoku board (board), row index (1), and column index (c) Output: list of all numbers that player is allowed to place on field (I, c), i.e., those that are not already present in row I, column c, and subgrid related to field (I, c) For example: >>> options (small2, 0, 0) [2, 3] >>> options (big, 6, 8) [3, 8] >>> options (giant2, 1, 5) [2, 5, 6, 9, 11, 12, 16] pass def hint (board) : Input : Sudoku board (board) Output: print board with a hint pass def play (board) : Input : Sudoku board Effect: Allows user to play board via console print board (board) while True: inp = input().split('') if len(inp) == 3 and inp[0].isdecimal() and inp[1].isdecimal() and inp [2 i = int(inp[0]) j = int(inp[1]) x = int(inp[2]) if x in options (board, i, j): board[i][j] = x else: print("Error print_board (board) elif len (inp) ==3 and (inp[0] == 'n' or inp[0] == 'new') and inp[1].isdec k = int(inp[1]) d = int(inp [2]) if k = 2: return res return res ###### A2 functions ############ ############ def inferred (board) : HHH Input : Sudoku board Output: new Soduko board with all values field from input board plus all values that can be inferred by repeated application of forward and backward single rule For example board big can be completely inferred: >>> inferred (big) # doctest: +NORMALIZE_WHITESPACE [/2, 1, 3, 4, 5, 6, 7, 8, 9 9], [4, 5, 6, 7, 8, 9, 1, 2, 3], PPPPPP [7, 8, 9, 1, 2, 3, 4, 5, 6], s''''' [1, 2, 4, 3, 6, 5, 8, 9, 7], P. [3, 6, 5, 8, 9, 7, 2, 1, 41, [8, 9, 7, 2, 1 1. 3, [5, 3, 1, 6, 6, 4, 2, 9, 7, 8], [6, 4, 2, 9, 7, 8, 5, 3, 1], [9, 7, 8, 5, 3, 1, 6, 4, 2]] 6, 51, But function doesn't modify input board: >>> big # doctest: +NORMALIZE_WHITESPACE [[0, 0, 0, 0, 0, 0, 0, 0, 0], [4, 0, 0, 7, 8, 9, 0, 0, 0], [7, 8, 0, 0, 0, 0, 0, 5, 6], 0 6, 0, 8, 0, 0], [0, 2, Oia o, 2 7, 0, 1, 0], [8, 0, 0, 2, 0, 0, 0, 0, 5], [0, 0, 1, 6, 4, 0, 9, 7, 0], [0, 0, 0, 9, 0, 0, 0, 0, 0], [0, 0, 0, 0, 3, 0, 0, 0, 2]] [0, 0, 5, 0. In board big4 there is nothing to infer: O, g, o, >>> inferred (big) # doctest: +NORMALIZE_WHITESPACE [[0, 0, 0, 6, 0, o, 2, 0, 0], [8, 0, 4, 0, 3, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], 14, 0, 5, 5, 0, 0, 0, 0, 0, 71, [7, 1, 1, 0, 0, 0, 0, 0, 0, 0], [0, 0, 3, 0, 5, 0, 0, 0, 8], [3, 0, 0, 0, 7, 0, 0, 0, 4], To, 0, 0, 0, 0. 9. 0. 01 Ln: 1 Co fields = sorted (fields, key=number_of_options) res = [] i, j = fields [0] opts = options (board, i, j) for o in opts: _board = copy.deepcopy (board) _board[i][j] = o res += solutions (_board) if len(res) >= 2: return res return res ########### A2 functions ############################# def inferred (board): Input : Sudoku board Output: new Soduko board with all values field from input board plus all values that can be inferred by repeated application of forward and backward single rule For example board big can be completely inferred: >>> inferred (big) # doctest: +NORMALIZE_WHITESPACE [[2, 1, 3, 4, 5, 6, 7, 8, 9], [4, 5, 6, 7, 8, 9, 1, 2, 3], [7, 8, 9, 1, 2, 3, 4, 5, [1, 2, 4, 3, 6, 5, 8. 9. 1. , , , 7), 13658972 41 [3, 6, 5, 8, 9, 7, 2, 1, 4], [8, 9, 7, 2, 1, 4, 3, 6, , 5], [5, 3, 1, 6, 4, 2, 9, 7, 8], 16, 4, 2, 9, 7, 8, 5, 3, 1], [9, 7, 8, 5, 3, 1, 6, 4, 2]] But function doesn't modify input board: >>> big # doctest: +NORMALIZE WHITESPACE [[0, 0, 0, 0, 0, 0, 0, 0, 0], [4, 0, 0, 7, 8, 9, 0, 0, 0], [7, 8, 0, 0, 0, 0, 0 0, 5, 6], [0, 2, 0, 3, 6, 0, 8, 0, 0], too jo [0, 0,5, 0, 0, 7, 0, 1, 0], [8, 0, 0, 2, 0, 0, 0, 0, 5], [0, 0, 1, 6, 4, 0, 1, 6, 4, 0, 9, 7, 0], [0, 0, 0, 9, 0, 0, 0, 0, 0], [0, 0, 0, 0, 3, 0, 0, 0, 2]] In board big4 there is nothing to infer: >>> inferred (big4) # doctest: +NORMALIZE_WHITESPACE [[0, 0, 0, 6, 0, 0, 2, 0, 0], [8, 0, 4, 0, 3, 0, 0, 0, 0], X' ' ' ' ' ' ' ' [0, 0, 0, 0, 0, 9, 0, 0, 0], [4, 0,5, 0, 0, 0, 0, 0, 7], [7, 1, 0, 0, 0, 0, 0, 0, 0], [0, 0, 3, 0,5, 0, 0, 0, 8], [3, 0, 0, 0, 7, 0, 0, 0, 41, [0, 0, 0, 0, 0, 1, 9, 0, 0], [0, 0, 0, 2, 0, 0, 0, 6, 0]] TH pass def generate (k): * Input : size of the board Output: new partially filled Soduko board that has unique solution For example: >>> len (solutions (generate (2))) i >>> len (solutions (generate (3))) i pass ########### Driver code (executed when running module) import doctest doctest.testmod (verbose=False)












