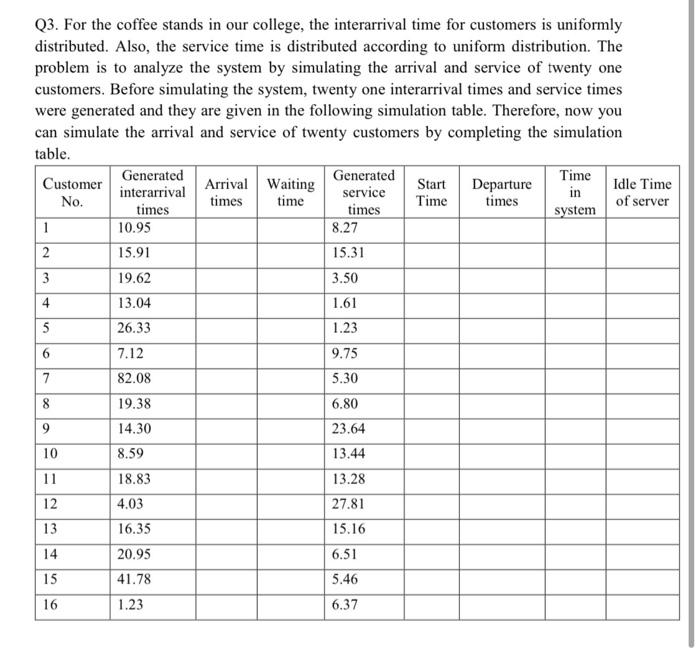
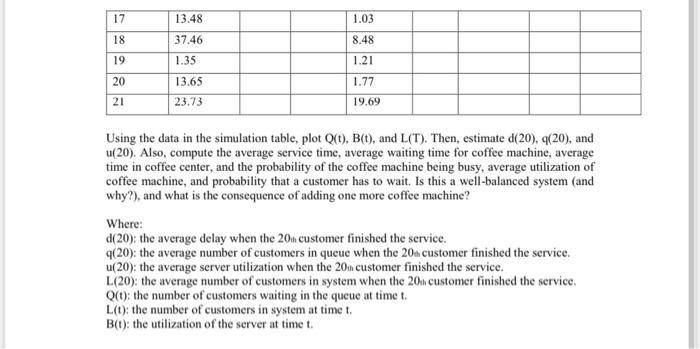
Q3. For the coffee stands in our college, the interarrival time for customers is uniformly distributed. Also, the service time is distributed according to uniform distribution. The problem is to analyze the system by simulating the arrival and service of twenty one customers. Before simulating the system, twenty one interarrival times and service times were generated and they are given in the following simulation table. Therefore, now you can simulate the arrival and service of twenty customers by completing the simulation table. Customer Generated Time Generated Arrival Waiting Start interarrival Departure service in Idle Time No. times time Time times of server times times system 10.95 8.27 2 15.91 15.31 3 19.62 3.50 13.04 1.61 5 26.33 1.23 7.12 9.75 7 82.08 5.30 19.38 6.80 14.30 23.64 1 4 6 8 9 10 8.59 13.44 11 18.83 13.28 12 27.81 4.03 16.35 13 15.16 14 20.95 6.51 15 41.78 5.46 16 1.23 6.37 17 13.48 1.03 18 8.48 37.46 1.35 19 1.21 20 13.65 1.77 21 23.73 19.69 Using the data in the simulation table, plot Q(t), B(t), and L(T). Then, estimated(20), 4(20), and (20). Also, compute the average service time, average waiting time for coffee machine, average time in coffee center, and the probability of the coffee machine being busy, average utilization of coffee machine, and probability that a customer has to wait. Is this a well-balanced system (and why?), and what is the consequence of adding one more coffee machine? Where: d(20): the average delay when the 20n customer finished the service. 9(20): the average number of customers in queue when the 20n customer finished the service. (20): the average server utilization when the 20n customer finished the service. L(20): the average number of customers in system when the 20n customer finished the service, Q(t): the number of customers waiting in the queue at time t. L(t): the number of customers in system at time t. B(t): the utilization of the server at time t. Q3. For the coffee stands in our college, the interarrival time for customers is uniformly distributed. Also, the service time is distributed according to uniform distribution. The problem is to analyze the system by simulating the arrival and service of twenty one customers. Before simulating the system, twenty one interarrival times and service times were generated and they are given in the following simulation table. Therefore, now you can simulate the arrival and service of twenty customers by completing the simulation table. Customer Generated Time Generated Arrival Waiting Start interarrival Departure service in Idle Time No. times time Time times of server times times system 10.95 8.27 2 15.91 15.31 3 19.62 3.50 13.04 1.61 5 26.33 1.23 7.12 9.75 7 82.08 5.30 19.38 6.80 14.30 23.64 1 4 6 8 9 10 8.59 13.44 11 18.83 13.28 12 27.81 4.03 16.35 13 15.16 14 20.95 6.51 15 41.78 5.46 16 1.23 6.37 17 13.48 1.03 18 8.48 37.46 1.35 19 1.21 20 13.65 1.77 21 23.73 19.69 Using the data in the simulation table, plot Q(t), B(t), and L(T). Then, estimated(20), 4(20), and (20). Also, compute the average service time, average waiting time for coffee machine, average time in coffee center, and the probability of the coffee machine being busy, average utilization of coffee machine, and probability that a customer has to wait. Is this a well-balanced system (and why?), and what is the consequence of adding one more coffee machine? Where: d(20): the average delay when the 20n customer finished the service. 9(20): the average number of customers in queue when the 20n customer finished the service. (20): the average server utilization when the 20n customer finished the service. L(20): the average number of customers in system when the 20n customer finished the service, Q(t): the number of customers waiting in the queue at time t. L(t): the number of customers in system at time t. B(t): the utilization of the server at time t