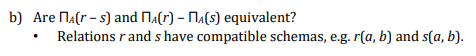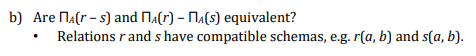
Query Optimization and Equivalence Rules (20 points) Using the relational algebra to specify queries can be tedious at times, but it also has a big benefit that there are many different ways to state a particular query. Although different versions will produce identical results, some versions can be evaluated much more quickly than others. For example, given this schema: store(store id, store_city, store_state) employee(emp id, emp_name, store_id, salary) Let's look at a query for finding the names of all employees who work in stores in Idaho, and make at least $70,000 a year. The relational algebra expression would look something like this: Memp_name(Ostore state = "10" A salary2 7000(store-employee)) However, if employee is a large relation then this query will be very slow to compute, even if very few tuples actually satisfy the selection criteria. What we would like the database to do is rearrange the query, producing an equivalent expression that will evaluate much faster, such as this: Memp_name(Ostore_state = "ID"(store) - Osalary 2 70000 (employee)) Note that we have broken the select operation into two separate operations, and we have rearranged the query so that these operations are applied before the join takes place. This ensures that the join will receive the smallest number of inputs possible. Good database engines will perform optimizations like this to make queries run faster; the better the database engine, the more kinds of optimizations it will know how to apply. Optimizations like these are driven by equivalence rules, which state that two relational algebra expressions are equivalent. In other words, given any legal database instance that is, a database that satisfies all primary/candidate and foreign key constraints), the two equivalent expressions would generate the exact same results. An example equivalence rule would be: Op1. p2(E) = Opion(E)) (conjunctive select operations can be deconstructed into a sequence of individual selections"). The book lists a number of equivalence rules in section 13.2.1. (Rule 7b in this section shows that the two queries given above are in fact equivalent.) Here are a number of potential equivalence rules; you must determine whether each pair of expressions is in fact equivalent. If the expressions are equivalent, give proof. (Your proof doesn't need to be rigorous, but you should be able to make it clear exactly why the expressions are equivalent.) If they are not equivalent, give a counterexample. Answers will only receive credit if b) Are Mar - s) and (Ar) - MA(s) equivalent? Relations r and s have compatible schemas, e.g. r(a, b) and s(a, b). . Query Optimization and Equivalence Rules (20 points) Using the relational algebra to specify queries can be tedious at times, but it also has a big benefit that there are many different ways to state a particular query. Although different versions will produce identical results, some versions can be evaluated much more quickly than others. For example, given this schema: store(store id, store_city, store_state) employee(emp id, emp_name, store_id, salary) Let's look at a query for finding the names of all employees who work in stores in Idaho, and make at least $70,000 a year. The relational algebra expression would look something like this: Memp_name(Ostore state = "10" A salary2 7000(store-employee)) However, if employee is a large relation then this query will be very slow to compute, even if very few tuples actually satisfy the selection criteria. What we would like the database to do is rearrange the query, producing an equivalent expression that will evaluate much faster, such as this: Memp_name(Ostore_state = "ID"(store) - Osalary 2 70000 (employee)) Note that we have broken the select operation into two separate operations, and we have rearranged the query so that these operations are applied before the join takes place. This ensures that the join will receive the smallest number of inputs possible. Good database engines will perform optimizations like this to make queries run faster; the better the database engine, the more kinds of optimizations it will know how to apply. Optimizations like these are driven by equivalence rules, which state that two relational algebra expressions are equivalent. In other words, given any legal database instance that is, a database that satisfies all primary/candidate and foreign key constraints), the two equivalent expressions would generate the exact same results. An example equivalence rule would be: Op1. p2(E) = Opion(E)) (conjunctive select operations can be deconstructed into a sequence of individual selections"). The book lists a number of equivalence rules in section 13.2.1. (Rule 7b in this section shows that the two queries given above are in fact equivalent.) Here are a number of potential equivalence rules; you must determine whether each pair of expressions is in fact equivalent. If the expressions are equivalent, give proof. (Your proof doesn't need to be rigorous, but you should be able to make it clear exactly why the expressions are equivalent.) If they are not equivalent, give a counterexample. Answers will only receive credit if b) Are Mar - s) and (Ar) - MA(s) equivalent? Relations r and s have compatible schemas, e.g. r(a, b) and s(a, b)