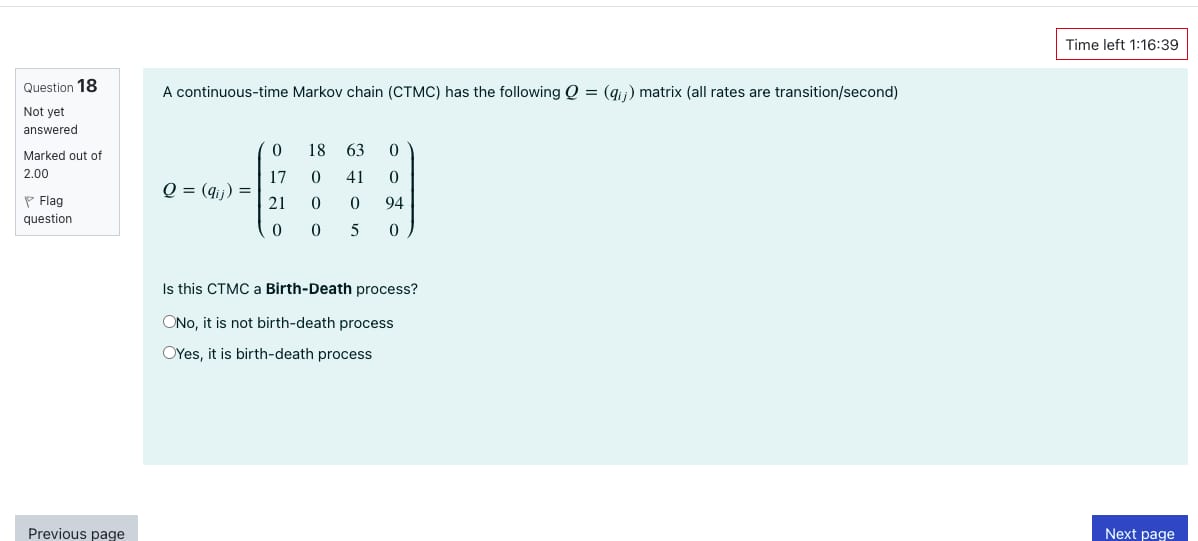
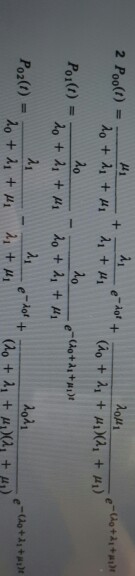
Question 18 Not yet answered Marked out of 2.00 Flag question A continuous-time Markov chain (CTMC) has the following Q = (q) matrix (all rates are transition/second) 0 18 63 0 17 0 41 0 Q = (qij) 21 0 0 94 0 0 5 0 Previous page Is this CTMC a Birth-Death process? ONo, it is not birth-death process OYes, it is birth-death process Time left 1:16:39 Next page Problem 2: 10 points Consider a birth-and-death process, X = {x(t): t 0}, associated with the service line that consists of N = 10 servers. When all 10 servers are occupied, the new request is refused and not coming into the service line. As there are k < 10 ongoing service requests, the next incoming request is going to occupy either of the vacant servers. This situation is described with the possible state space, S={0, 1, 2, ..., 10} and the infinitesimal transition probabilities (as A0) are described as follows: P[X(t+A)X(t) = 1|x(t)=k] = = 3 (10-k) for 0 k 10, and = 0 for k > 10, and P[X(t+A)-x(t)=-1|x(t)=k] =k=2. k for 0 k 10. 1. Derive the stationary distribution of the number of ongoing service requests, for 0 k 10. lim P[X(t)=k], 80+7 2. Determine the limiting probability of the idle state, x = 0, that is: lim P[X(t) = 0] 3. Determine the limiting probability of having all servers occupied: lim P[X(t) =10] 8047 2 Poo(t) = Poi(t) = = 20 + 2 + 1 20 + 21 +11 21 + e-do + e-Co+1+1) 2 + 1 (do++)(2 + #) 20 - 20+ 2 + 1 21 Poz(t) e-dor + 20 + 21+ #1 2+1 (20+2+)(2 +4)