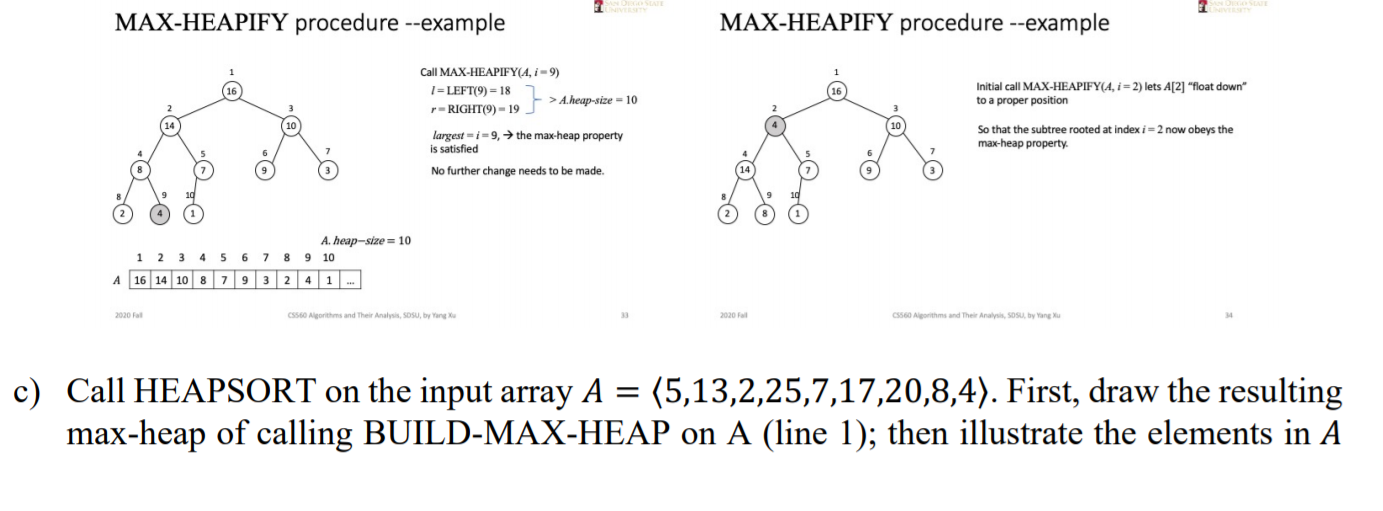
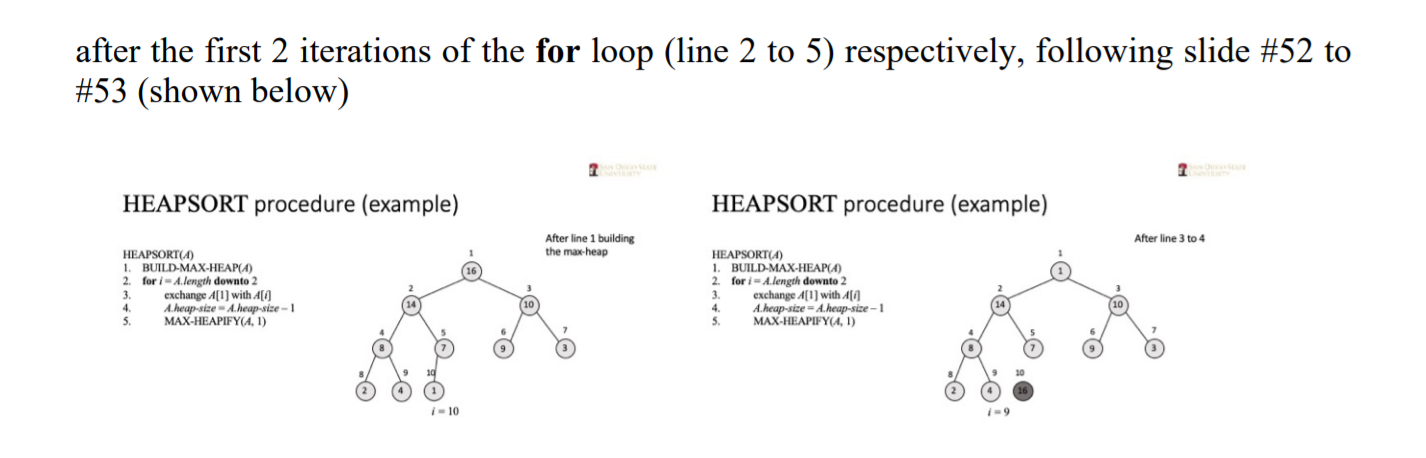
Question 2 (3.5 points) Heapsort a) Is the array with values (23,17,14,6,13,10,1,5,7,12) a max-heap? Draw the tree-like plot, and identify the nodes that violate the max-heap property. on b) Using the plots on slide #31 to #34 (shown in figures below) as a model, illustrate the final outcome of calling MAX-HEAPIFY(A, 3) the input array: A = (27,17,3,16,13,10,1,5,7,12,4,8,9,0). (Just need to draw two heap plots, one before the calling and one after.) MAX-HEAPIFY procedure -- example MAX-HEAPIFY procedure -- example Call MAX-HEAPIFYA, - 2) 1-LEFT(2) - 4 RIGHT(2) 5 A[4] > A[5] > A[2] largest = 4, the subtree rooted at A[2] violates the max-heap property Needs to exchange A[4) with A[2] And then call MAX-HEAPIFYA, 4) Call MAX-HEAPIFYCA, 1-4) 1 = LEFT(4) = 8 r=RIGHT(4) = 9 A[9] > A[4] > A[8] largest = 9, the subtree rooted at A[4] violates the max-heap property Needs to exchange A[9] with A[4] And then call MAX-HEAPIFY(A, 9) 14 1 2 4 5 6 7 8 9 10 A. heap-size = 10 2 3 4 5 6 7 8 9 10 A 16 4 10 14 7 9 3 2 8 1 .. A 16 14 10 4 7 9 3 2 8 1 2020 Rall C5560 Algorithms and Their Analysis, SOSU, by Yong Xu 2020 Fall CSSO Algorithms and Their Analysis, SOSU, by Yong Xu LE TE MAX-HEAPIFY procedure --example MAX-HEAPIFY procedure --example Call MAX-HEAPIFY(A, i -9) 1 =LEFT(9) = 18 > A.heap-size = 10 -RIGHT(9) - 19 Initial call MAX-HEAPIFY(A, i = 2) lets A[2] "float down" to a proper position So that the subtree rooted at index i = 2 now obeys the max-heap property. largest 1-9, the max-heap property is satisfied No further change needs to be made. A heap-size = 10 9 10 3 4 5 6 7 8 A 16 14 10 87932 41 2020 Ft C5560 Algorithms and Their Analysis, SOSU, by Yong Xu 2020 65560 A conths and The Analys, SOS by Yangu = c) Call HEAPSORT on the input array A - (5,13,2,25,7,17,20,8,4). First, draw the resulting max-heap of calling BUILD-MAX-HEAP on A (line 1); then illustrate the elements in A after the first 2 iterations of the for loop (line 2 to 5) respectively, following slide #52 to #53 (shown below) HEAPSORT procedure (example) HEAPSORT procedure (example) After line 3 to 4 After line 1 building the max-heap HEAPSORT(4) 1. BUILD-MAX-HEAP(A) 2. fori - A.length downto 2 3. exchange A[1] with AO A.heap-size - A heap-size-1 5 MAX-HEAPIFY (1) HEAPSORT(A) 1. BUILD-MAX-HEAP(A) 2. for i = 4.length downto 2 3 exchange A[1] with A[ A.heap-size = A.heap-size-1 5 MAX-HEAPIFYA, 1) (10 4. 8 1-10