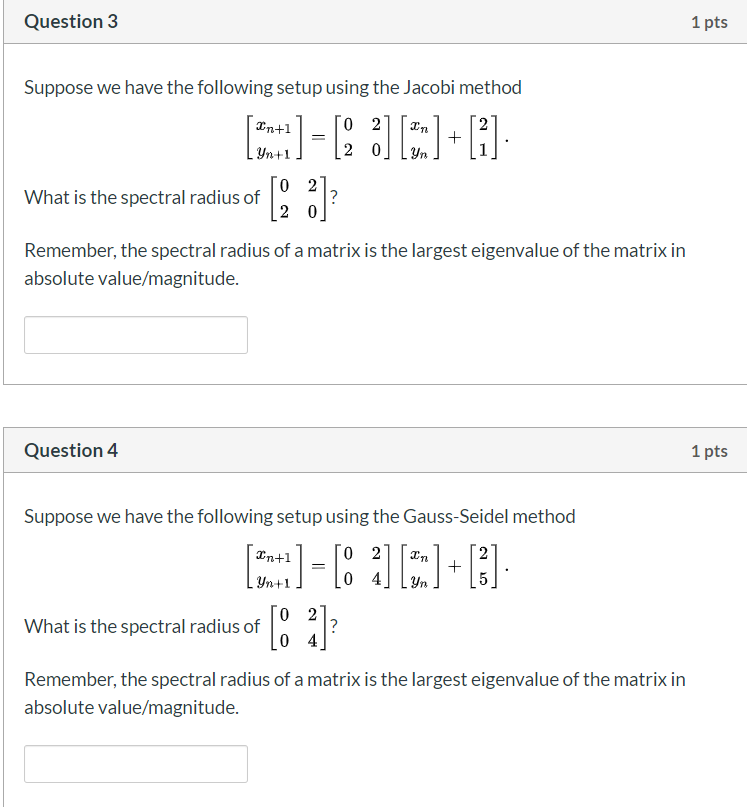
Question 3 1 pts Suppose we have the following setup using the Jacobi method What is the spectral radius of 12 0 2 Remember, the spectral radius of a matrix is the largest eigenvalue of the matrix in absolute value/magnitude. Question 4 1 pts Suppose we have the following setup using the Gauss-Seidel method and]= [8 2] [am]+ [3]. What is the spectral radius of 6 2 ? Remember, the spectral radius of a matrix is the largest eigenvalue of the matrix in absolute value/magnitude.5. (a) State the Spectral Theorem for Symmetric matrices. (b) Write out the spectral factorization of 5 2 A = 2 2 (c) Using the change of variables x = Qy, where Q is an appropriate orthogonal matric, express the quadratic form 5r, + 4r142 + 21% in terms of y and y2. Describe and sketch the graph of the equation 5r, + 4712 + 2x2 = 1 in the T1, 12 plane. (d) Find the spectral decomposition of A.3. An ice cream shop has three flavors - vanilla, chocolate, and strawberry. Vanilla ice creams are sold as Poisson Process with rate of 3 per hour. Chocolate ice creams are sold as Poisson Process with rate of 4 per hour. Strawberry ice creams are sold as Poisson Process with rate of 2 per hour. (a) What is the probability that the ice cream shop will sell 10 ice creams between 4:00 - 5:00 pm? (b) 20% of the shop's customers are senior citizens. What is the probability that the shop will sell 8 ice creams to senior citizens between 12:00 - 4:00 pm?5. Poisson processes (a) Give the probability that there are exactly 3 arrivals in a time interval of length 2 for a Poisson process of intensity A. (b) Give the expected inter-arrival time for a Poisson process of intensity 5. (c) Explain what it means that increments are stationary for a Poisson process.Consider a Markov chain {Xn : n = 0, 1, 2, ...} with state space {1, 2, 3} and one-step transition probability matrix O NIH NIH P = O 0 O (a) Mark O or X: ( ) The Markov chain is irreducible. ( ) The Markov chain is aperiodic. ( ) The Markov chain is transient. ( ) The Markov chain is recurrent. ( ) The Markov chain is null recurrent. ( ) The Markov chain is ergodic. (b) Calculate P(X5 = 1/X2 = 1). (c) Find limn + P(Xn = 1/X2 = 1)