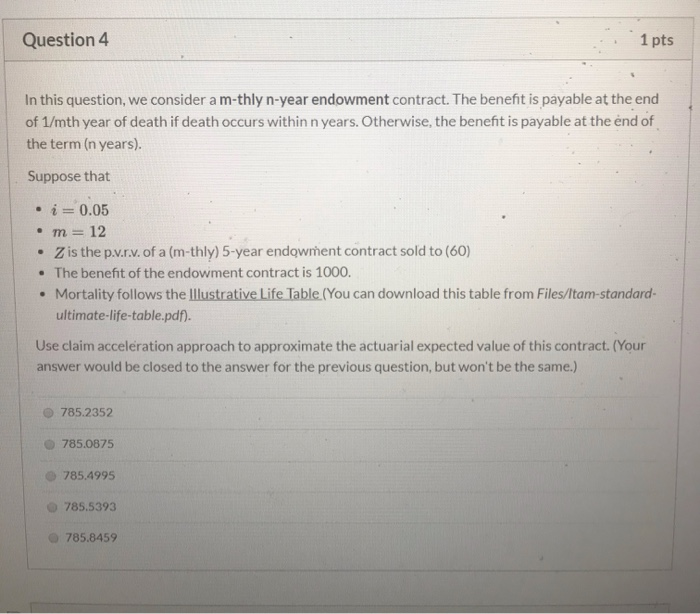
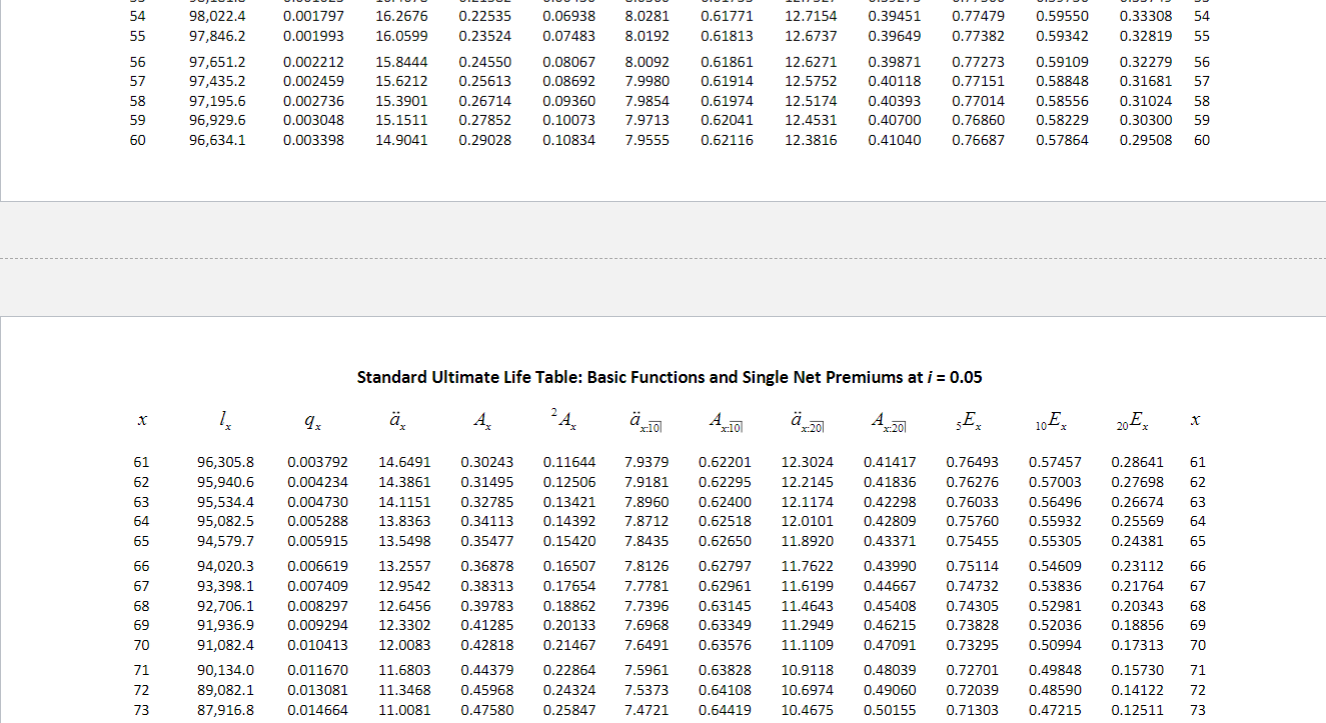
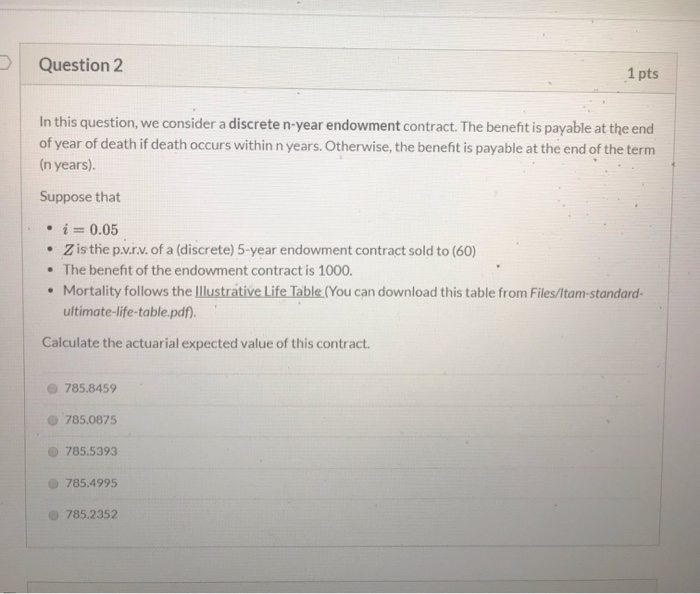
Question 4 1 pts In this question, we consider a m-thly n-year endowment contract. The benefit is payable at the end of 1/mth year of death if death occurs within n years. Otherwise, the benefit is payable at the end of the term (n years). Suppose that . i = 0.05 m = 12 . Z is the p...r.v. of a (m-thly) 5-year endowment contract sold to (60) The benefit of the endowment contract is 1000. Mortality follows the Illustrative Life Table (You can download this table from Files/Itam-standard- ultimate-life-table.pdf). Use claim acceleration approach to approximate the actuarial expected value of this contract. (Your answer would be closed to the answer for the previous question, but won't be the same.) 785.2352 785.0875 785.4995 785.5393 785.8459 98,022.4 97,846.2 16.2676 16.0599 97,651.2 97,435.2 97,195.6 96,929.6 96,634.1 0.001797 0.001993 0.002212 0.002459 0.002736 0.003048 0.003398 15.8444 15.6212 15.3901 15.1511 14.9041 0.22535 0.23524 0.24550 0.25613 0.26714 0.27852 0.29028 0.06938 8.0281 0.07483 8.0192 0.08067 8.0092 0.08692 7.9980 0.09360 7.9854 0.100737.9713 0.10834 7.9555 0.61771 0.61813 0.61861 0.61914 0.61974 0.62041 0.62116 12.7154 12.6737 12.6271 12.5752 12.5174 12.4531 12.3816 0.39451 0.77479 0.59550 0.33308 54 0.39649 0.77382 0.59342 0.3281955 0.398710.772730.591090.3227956 0.40118 0.77151 0.58848 0.31681 57 0.40393 0.77014 0.58556 0.31024 58 0.40700 0.768600.58229 0.30300 59 0.41040 0.766870.57864 0.29508 60 Standard Ultimate Life Table: Basic Functions and Single Net Premiums at i = 0.05 & zo 410 zo 420 Ex 10E 20Ex x 96,305.8 95,940.6 95,534.4 95,082.5 94,579.7 94,020.3 93,398.1 92,706.1 91,936.9 91,082.4 90,134.0 89,082.1 87,916.8 0.003792 0.004234 0.004730 0.005288 0.005915 0.006619 0.007409 0.008297 0.009294 0.010413 0.011670 0.013081 0.014664 14.6491 14.3861 14.1151 13.8363 13.5498 13.2557 12.9542 12.6456 12.3302 12.0083 11.6803 11.3468 11.0081 0.30243 0.116447.93790.62201 12.3024 0.41417 0.76493 0.574570.28641 61 0.31495 0.125067.9181 0.62295 12.2145 0.41836 0.76276 0.570030.27698 62 0.32785 0.13421 7.8960 0.62400 12.1174 0.42298 0.76033 0.56496 0.26674 0.34113 0.14392 7.8712 0.62518 12.0101 0.42809 0.75760 0.55932 0.25569 0.35477 0.15420 7.8435 0.62650 11.8920 0.43371 0.75455 0.55305 0.24381 0.36878 0.16507 7.8126 0.62797 11.7622 0.43990 0.75114 0.54609 0.23112 66 0.38313 0.17654 7.7781 0.62961 11.6199 0.44667 0.74732 0.53836 0.21764 0.39783 0.18862 7.7396 0.6314511.4643 0.454080.74305 0.52981 0.2034368 0.41285 0.20133 7.6968 0.63349 11.2949 0.46215 0.73828 0.52036 0.18856 0.42818 0.21467 7.6491 0.63576 11.11090.470910.73295 0.50994 0.17313 70 0.443790.228647.5961 0.63828 10.9118 0.48039 0.72701 0.498480.15730 71 0.45968 0.243247.5373 0.64108 10.6974 0.49060 0.720390.48590 0.14122 72 0.47580 0.25847 7.4721 0.64419 10.4675 0.50155 0.71303 0.47215 0.12511 73 69 Question 2 1 pts In this question, we consider a discrete n-year endowment contract. The benefit is payable at the end of year of death if death occurs within n years. Otherwise, the benefit is payable at the end of the term (n years). Suppose that . i = 0.05 Z is the p.v.r.v. of a (discrete) 5-year endowment contract sold to (60) The benefit of the endowment contract is 1000. Mortality follows the Illustrative Life Table (You can download this table from Files/Itam-standard- ultimate-life-table.pdf). Calculate the actuarial expected value of this contract. 785.8459 785.0875 785.5393 785.4995 785.2352 Question 4 1 pts In this question, we consider a m-thly n-year endowment contract. The benefit is payable at the end of 1/mth year of death if death occurs within n years. Otherwise, the benefit is payable at the end of the term (n years). Suppose that . i = 0.05 m = 12 . Z is the p...r.v. of a (m-thly) 5-year endowment contract sold to (60) The benefit of the endowment contract is 1000. Mortality follows the Illustrative Life Table (You can download this table from Files/Itam-standard- ultimate-life-table.pdf). Use claim acceleration approach to approximate the actuarial expected value of this contract. (Your answer would be closed to the answer for the previous question, but won't be the same.) 785.2352 785.0875 785.4995 785.5393 785.8459 98,022.4 97,846.2 16.2676 16.0599 97,651.2 97,435.2 97,195.6 96,929.6 96,634.1 0.001797 0.001993 0.002212 0.002459 0.002736 0.003048 0.003398 15.8444 15.6212 15.3901 15.1511 14.9041 0.22535 0.23524 0.24550 0.25613 0.26714 0.27852 0.29028 0.06938 8.0281 0.07483 8.0192 0.08067 8.0092 0.08692 7.9980 0.09360 7.9854 0.100737.9713 0.10834 7.9555 0.61771 0.61813 0.61861 0.61914 0.61974 0.62041 0.62116 12.7154 12.6737 12.6271 12.5752 12.5174 12.4531 12.3816 0.39451 0.77479 0.59550 0.33308 54 0.39649 0.77382 0.59342 0.3281955 0.398710.772730.591090.3227956 0.40118 0.77151 0.58848 0.31681 57 0.40393 0.77014 0.58556 0.31024 58 0.40700 0.768600.58229 0.30300 59 0.41040 0.766870.57864 0.29508 60 Standard Ultimate Life Table: Basic Functions and Single Net Premiums at i = 0.05 & zo 410 zo 420 Ex 10E 20Ex x 96,305.8 95,940.6 95,534.4 95,082.5 94,579.7 94,020.3 93,398.1 92,706.1 91,936.9 91,082.4 90,134.0 89,082.1 87,916.8 0.003792 0.004234 0.004730 0.005288 0.005915 0.006619 0.007409 0.008297 0.009294 0.010413 0.011670 0.013081 0.014664 14.6491 14.3861 14.1151 13.8363 13.5498 13.2557 12.9542 12.6456 12.3302 12.0083 11.6803 11.3468 11.0081 0.30243 0.116447.93790.62201 12.3024 0.41417 0.76493 0.574570.28641 61 0.31495 0.125067.9181 0.62295 12.2145 0.41836 0.76276 0.570030.27698 62 0.32785 0.13421 7.8960 0.62400 12.1174 0.42298 0.76033 0.56496 0.26674 0.34113 0.14392 7.8712 0.62518 12.0101 0.42809 0.75760 0.55932 0.25569 0.35477 0.15420 7.8435 0.62650 11.8920 0.43371 0.75455 0.55305 0.24381 0.36878 0.16507 7.8126 0.62797 11.7622 0.43990 0.75114 0.54609 0.23112 66 0.38313 0.17654 7.7781 0.62961 11.6199 0.44667 0.74732 0.53836 0.21764 0.39783 0.18862 7.7396 0.6314511.4643 0.454080.74305 0.52981 0.2034368 0.41285 0.20133 7.6968 0.63349 11.2949 0.46215 0.73828 0.52036 0.18856 0.42818 0.21467 7.6491 0.63576 11.11090.470910.73295 0.50994 0.17313 70 0.443790.228647.5961 0.63828 10.9118 0.48039 0.72701 0.498480.15730 71 0.45968 0.243247.5373 0.64108 10.6974 0.49060 0.720390.48590 0.14122 72 0.47580 0.25847 7.4721 0.64419 10.4675 0.50155 0.71303 0.47215 0.12511 73 69 Question 2 1 pts In this question, we consider a discrete n-year endowment contract. The benefit is payable at the end of year of death if death occurs within n years. Otherwise, the benefit is payable at the end of the term (n years). Suppose that . i = 0.05 Z is the p.v.r.v. of a (discrete) 5-year endowment contract sold to (60) The benefit of the endowment contract is 1000. Mortality follows the Illustrative Life Table (You can download this table from Files/Itam-standard- ultimate-life-table.pdf). Calculate the actuarial expected value of this contract. 785.8459 785.0875 785.5393 785.4995 785.2352