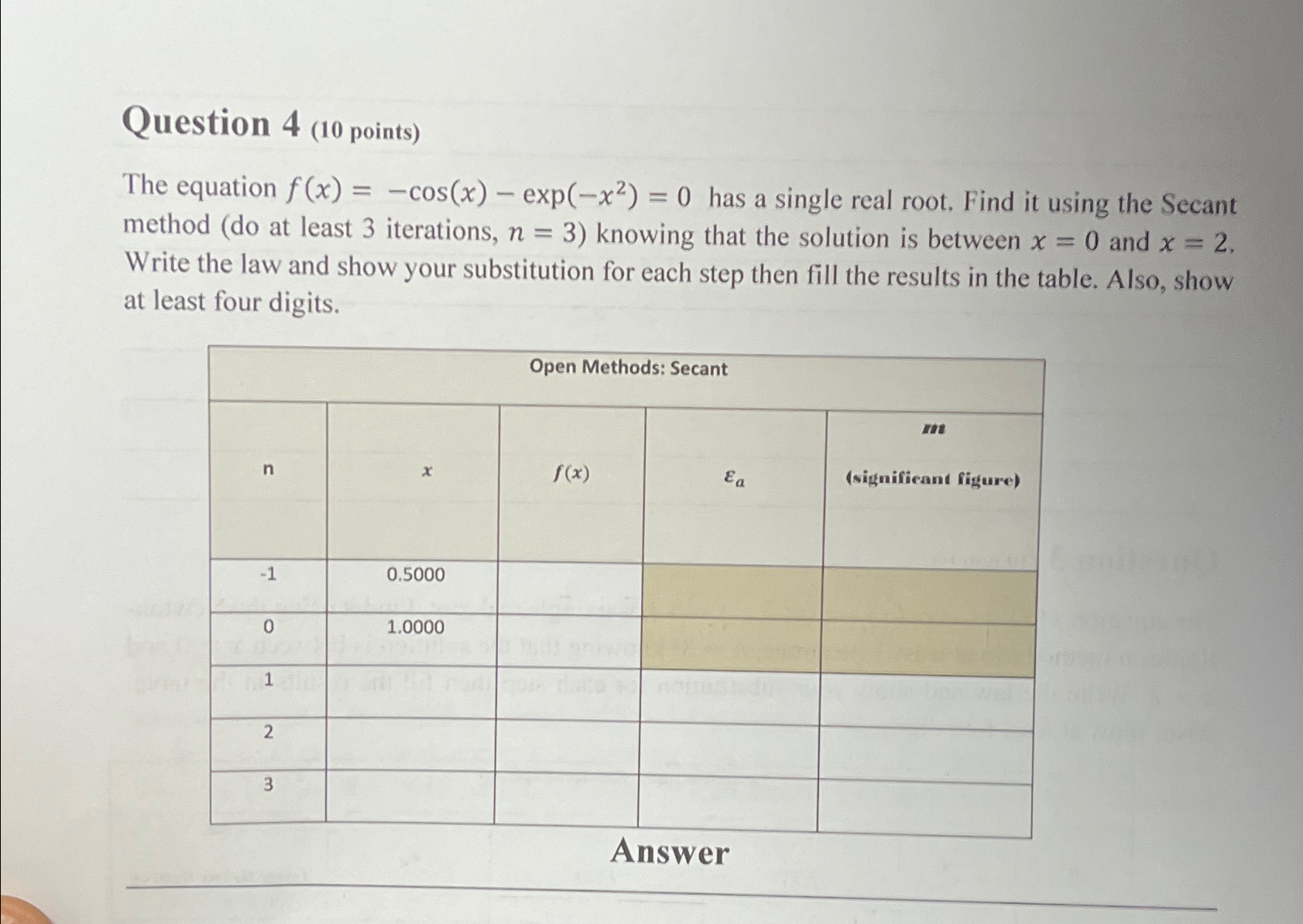
Question: Question 4 (10 points) The equation f(x)=-cos(x)-exp(-x^(2))=0 has a single real root. Find it using the Secant method (do at least 3 iterations, n=3 )
Question 4 (10 points)\ The equation
f(x)=-cos(x)-exp(-x^(2))=0has a single real root. Find it using the Secant method (do at least 3 iterations,
n=3) knowing that the solution is between
x=0and
x=2. Write the law and show your substitution for each step then fill the results in the table. Also, show at least four digits.\ \\\\table[[Open Methods: Secant],[
n,
x,
f(x),
\\\\epsi _(a),(signifient figure)],[-1,0.5000,,,],[0,1.0000,,,],[1,,,,],[2,,,,],[3,,,,]]\ Answer
The equation f(x)=cos(x)exp(x2)=0 has a single real root. Find it using the Secant method (do at least 3 iterations, n=3 ) knowing that the solution is between x=0 and x=2, Write the law and show your substitution for each step then fill the results in the table. Also, show at least four digits
Step by Step Solution
There are 3 Steps involved in it
To solve the equation fx cosx expx2 0 using the Secant method follow these steps The secant method f... View full answer

Get step-by-step solutions from verified subject matter experts


