Question
Question 7(3 points) A pool of the shape of an inverted truncated pyramid as shown in the following figure is filled with water up to

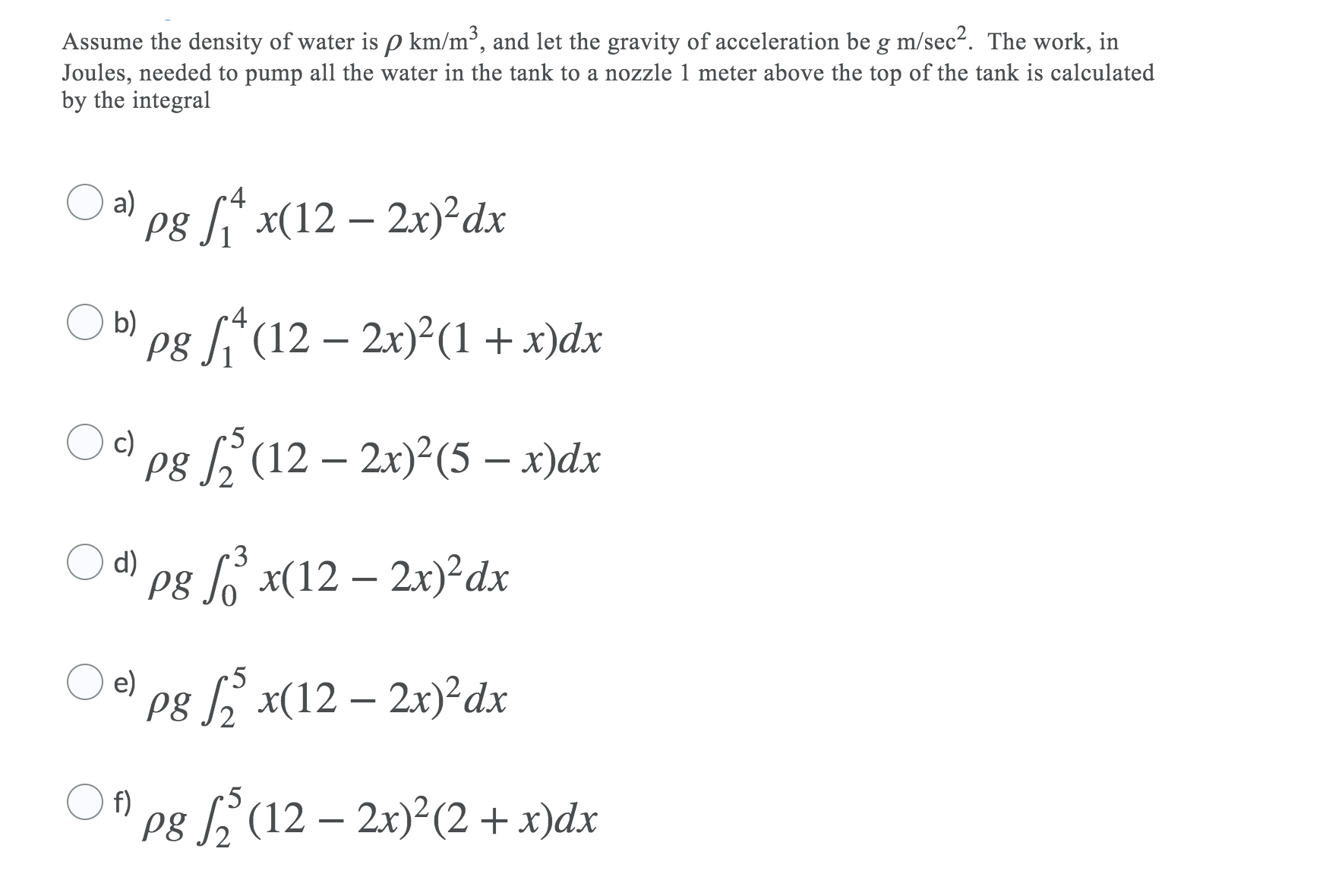
Question 7(3 points)
A pool of the shape of an inverted truncated pyramid as shown in the following figure is filled with water up to 3 meters deep.The top of the pool is a square of side-length 10 meters, the bottom of the pool is a square of side-length 2 maters, and the depth of the pool is 4 meters.The area of a horizontal layer of waterxmeters under the nozzle isA(x) = (12
{"version":"1.1","math":""}2x)2m2.
See this figure.
Assume the density of water is
{"version":"1.1","math":""}km/m3, and let the gravity of acceleration begm/sec2.The work, in Joules, needed to pump all the water in the tank to a nozzle 1 meter above the top of the tank is calculated by the integral
Question 7 options:
a)
g
4
1
x(122x)
2
dx
{"version":"1.1","math":"\( ho g\int_1^4 x(12-2x)^2dx\)"}
b)
g
4
1
(122x)
2
(1+x)dx
{"version":"1.1","math":"\( ho g\int_1^4 (12-2x)^2(1+x)dx\)"}
c)
g
5
2
(122x)
2
(5x)dx
{"version":"1.1","math":"\( ho g\int_2^5 (12-2x)^2(5-x)dx\)"}
d)
g
3
0
x(122x)
2
dx
{"version":"1.1","math":"\( ho g\int_0^3 x(12-2x)^2dx\)"}
e)
g
5
2
x(122x)
2
dx
{"version":"1.1","math":"\( ho g\int_2^5 x(12-2x)^2dx\)"}
f)
g
5
2
(122x)
2
(2+x)dx

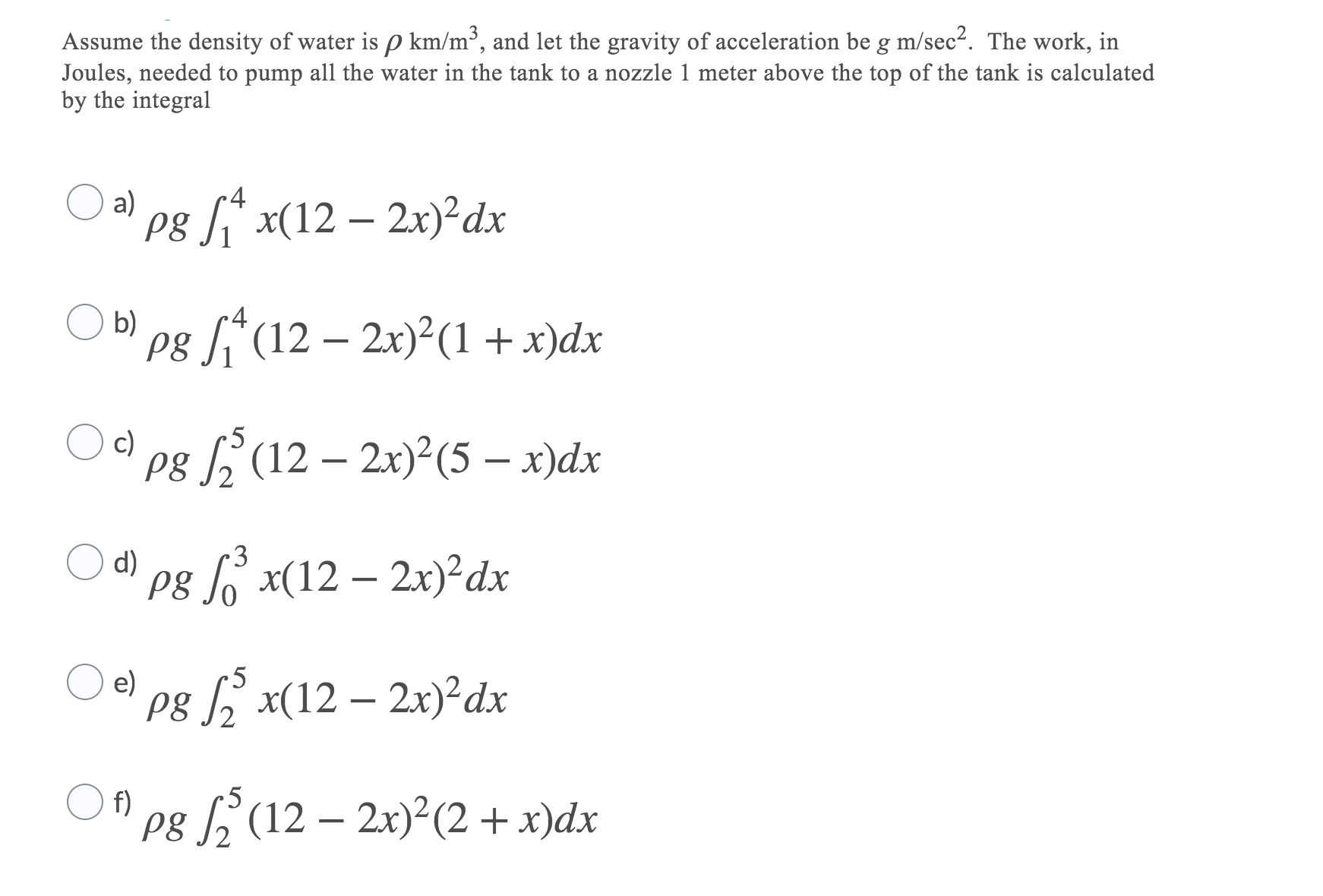
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


