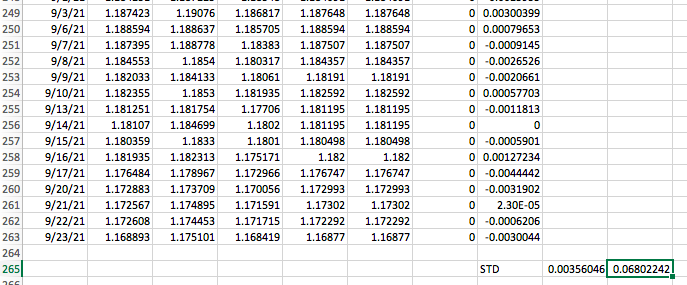
Question: Calculate EUR/USD call option premium, Exercise price = 11750 , expiration = Week 1 Oct; T= days til Oct/365, STD= 0.003560456, annual STD = 0.068022421, spot rate = 0.009107,

Formula:

Example:

249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 20 9/3/21 9/6/21 9/7/21 9/8/21 9/9/21 9/10/21 9/13/21 9/14/21 9/15/21 9/16/21 9/17/21 9/20/21 9/21/21 9/22/21 9/23/21 1.187423 1.188594 1.187395 1.184553 1.182033 1.182355 1.181251 1.18107 1.180359 1.181935 1.176484 1.172883 1.172567 1.172608 1.168893 1.19076 1.188637 1.188778 1.1854 1.184133 1.1853 1.181754 1.184699 1.1833 1.182313 1.178967 1.173709 1.174895 1.174453 1.175101 1.186817 1.185705 1.18383 1.180317 1.18061 1.181935 1.17706 1.1802 1.1801 1.175171 1.172966 1.170056 1.171591 1.171715 1.168419 1.187648 1.188594 1.187507 1.184357 1.18191 1.182592 1.181195 1.181195 1.180498 1.182 1.176747 1.172993 1.17302 1.172292 1.16877 1.187648 1.188594 1.187507 1.184357 1.18191 1.182592 1.181195 1.181195 1.180498 1.182 1.176747 1.172993 1.17302 1.172292 1.16877 0 0.00300399 0 0.00079653 0 -0.0009145 0 -0.0026526 0 -0.0020661 0 0.00057703 0 -0.0011813 0 0 0 -0.0005901 0 0.00127234 0 -0.0044442 0 -0.0031902 0 2.30E-05 0 -0.0006206 0 -0.0030044 STD 0.00356046 0.06802242 The basic theoretical model for the pricing of a European call option is C = e = {T SN (dz) Ee="dl N (da) Where C =premium on a European call e=continuous time discounting S =spot exchange rate ($/foreign currency) E=exercise or strike rate T=time to expiration N =cumulative normal distribution function rf=foreign interest rate ra=domestic interest rate o=standard deviation of asset price (volatility) In =natural logarithm + The two density functions, dj and d2, are defined as In (1) + (ra=rs+)1 di = OVT and d2 = di - OVT This expression can be rearranged so the premium on a European call option is written in terms of the forward rate: Cre=rFN (di) raT e EN (d2) where the spot rate and foreign interest rate have been replaced with the forward rate, F, and both the first and second terms are discounted over continuous time, e. If we now slightly simplify, we find that the option premium is the present value of the difference between two cumulative normal density functions. C = [FN (d) EN (da)]e=T&T The two density functions are now defined as + In() di = OVT Spot rate $1.7000/ 90-day Forward = $1.7000/ Strike rate = $1.7000/ U.S. dollar interest rate = 8.00% (per annum) Pound sterling interest rate = 8.00% (per annum) Time (days) = 90 Std. Dev. (volatility) = 10.00% e (infinite discounting) = 2.71828 The value of the two density functions are first derived: In()+(Tin(:0) + (1.109) + 90 365 di = 0.025 OVT 0.1000 90 365 and dz = 0.025 - 0.1000 90 = -0.025 365 The values of di and d2 are then found in a cumulative normal probability table: N (di) = N(0.025) = 0.51; N(d2) = (- 0.025) = 0.49 The premium of the European call with a forward-at-the-money" strike rate is C = [(1.7000) (.51) (1.7000) (0.49)]2.718280.08(90/365) = $0.033/ 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 20 9/3/21 9/6/21 9/7/21 9/8/21 9/9/21 9/10/21 9/13/21 9/14/21 9/15/21 9/16/21 9/17/21 9/20/21 9/21/21 9/22/21 9/23/21 1.187423 1.188594 1.187395 1.184553 1.182033 1.182355 1.181251 1.18107 1.180359 1.181935 1.176484 1.172883 1.172567 1.172608 1.168893 1.19076 1.188637 1.188778 1.1854 1.184133 1.1853 1.181754 1.184699 1.1833 1.182313 1.178967 1.173709 1.174895 1.174453 1.175101 1.186817 1.185705 1.18383 1.180317 1.18061 1.181935 1.17706 1.1802 1.1801 1.175171 1.172966 1.170056 1.171591 1.171715 1.168419 1.187648 1.188594 1.187507 1.184357 1.18191 1.182592 1.181195 1.181195 1.180498 1.182 1.176747 1.172993 1.17302 1.172292 1.16877 1.187648 1.188594 1.187507 1.184357 1.18191 1.182592 1.181195 1.181195 1.180498 1.182 1.176747 1.172993 1.17302 1.172292 1.16877 0 0.00300399 0 0.00079653 0 -0.0009145 0 -0.0026526 0 -0.0020661 0 0.00057703 0 -0.0011813 0 0 0 -0.0005901 0 0.00127234 0 -0.0044442 0 -0.0031902 0 2.30E-05 0 -0.0006206 0 -0.0030044 STD 0.00356046 0.06802242 The basic theoretical model for the pricing of a European call option is C = e = {T SN (dz) Ee="dl N (da) Where C =premium on a European call e=continuous time discounting S =spot exchange rate ($/foreign currency) E=exercise or strike rate T=time to expiration N =cumulative normal distribution function rf=foreign interest rate ra=domestic interest rate o=standard deviation of asset price (volatility) In =natural logarithm + The two density functions, dj and d2, are defined as In (1) + (ra=rs+)1 di = OVT and d2 = di - OVT This expression can be rearranged so the premium on a European call option is written in terms of the forward rate: Cre=rFN (di) raT e EN (d2) where the spot rate and foreign interest rate have been replaced with the forward rate, F, and both the first and second terms are discounted over continuous time, e. If we now slightly simplify, we find that the option premium is the present value of the difference between two cumulative normal density functions. C = [FN (d) EN (da)]e=T&T The two density functions are now defined as + In() di = OVT Spot rate $1.7000/ 90-day Forward = $1.7000/ Strike rate = $1.7000/ U.S. dollar interest rate = 8.00% (per annum) Pound sterling interest rate = 8.00% (per annum) Time (days) = 90 Std. Dev. (volatility) = 10.00% e (infinite discounting) = 2.71828 The value of the two density functions are first derived: In()+(Tin(:0) + (1.109) + 90 365 di = 0.025 OVT 0.1000 90 365 and dz = 0.025 - 0.1000 90 = -0.025 365 The values of di and d2 are then found in a cumulative normal probability table: N (di) = N(0.025) = 0.51; N(d2) = (- 0.025) = 0.49 The premium of the European call with a forward-at-the-money" strike rate is C = [(1.7000) (.51) (1.7000) (0.49)]2.718280.08(90/365) = $0.033/