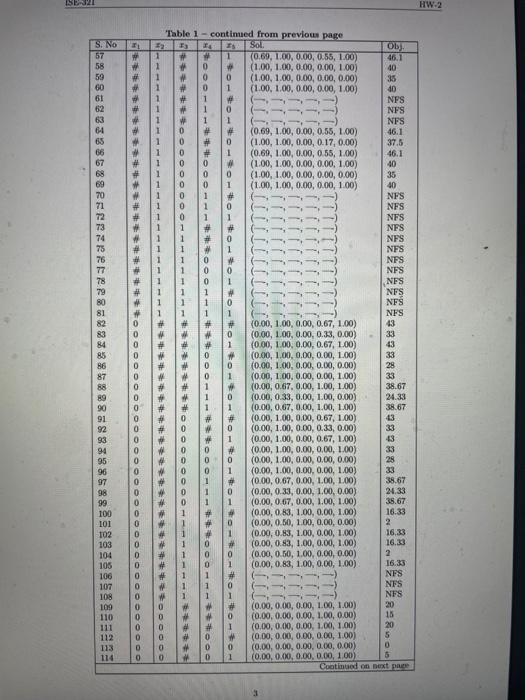
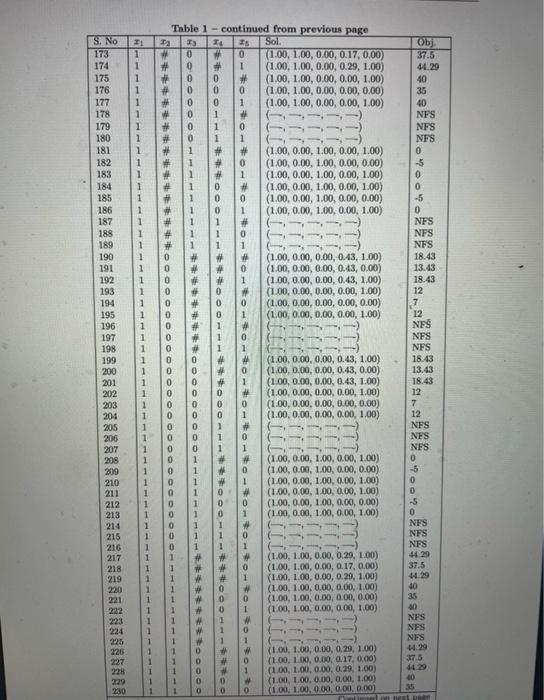
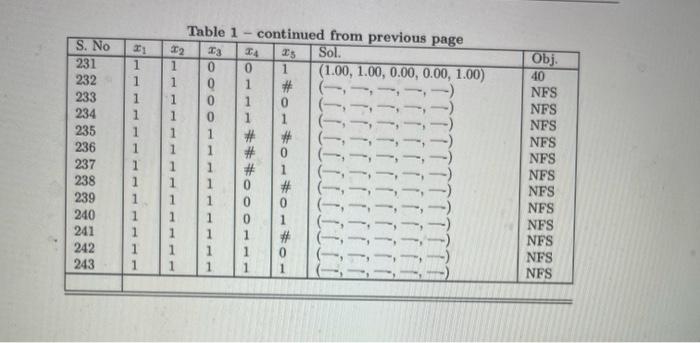
Questions are on the first image, the other images are all tables needed for question b&c

Consider the following IP problem. maximize:7x1+28x212x3+15x4+5x5subjectto:50+x170x2+40x4+30x430x310010x1+60x2+50+x3+60+x420x5806+x1+1+x2+3x3+7+x49xi{0,1}i=1,,5 (a) Write the LP relaxation of the above model. (b) Get the optimal objective function value of the L.P relaxation frotn Table 1. Is it a lower or an. upper botud? Explain. (c) Is x=[1,0,0,0,1]T a feasible solution to the above problen. If yes, then obtain its objective function value from Table 1. Is it a kower or an upper boumd? Explain. Solve the above problem wsing branch \& bound method, and bexild the euumeration tree using the following strategies. You can use the information from Table 1. Note: Generate ene tree for Pert (d), one for Part (e) and one for Part (f). Draw inside cach nodc, the node number. Neat to each node write objective function nuhe and all the froctional cariables. Draa the branch doun (or bounds) on the left side, and the branch up (or ) bounds on the right aide. While gencnating the tres, you should follow the strategies as deseribed. During the erecution of any strutegy, if the namber of nodes processed is greater than or cyual to 20 , then you can terminate the strulegy. Riport the incambent solution. Alvo, say in percentage, how far it is from the best possible solution. For Strategy-1, write the LP formulation that was soleed at every 5th node- (d) Strategy-1: - Node Selection: Best First Select the node with the best objective function value. - Variable Sebection: Nearest to integer A fructional variable with fractional value nearest to an integer will be used for branching- - Branching Direction: Up Select the branch of side (lower bound is increasod.) (e) Strategy-2: - Node Selection: Depth First the Best Back Select the most recently created child node to solve. If no child exists, then backtrack to the best bound node awalsble in the eatire tree. - Variable Selection: Lowest fraction A fractional variable with lowest fraction will be used for brapching- - Branchaing Direction: Down Select the branch of side (upper bound is decreased.) (f) Strategy-3: - Node Selectiot: Breadth Finst the Best Next All nodes at one level of the search tree are processed before any uode at a deeper hevel. In a given level, best node should be processed first. - Variable Selection: Highest fraction A fractional variable with highest fraction will be used for branching. - Branching Direction: You are froe to piok any rule. Thhk It Optimal Solutions for NII LP Relasetions, if Indicates Table 1 - continued from previous page Thhle 1 Consider the following IP problem. maximize:7x1+28x212x3+15x4+5x5subjectto:50+x170x2+40x4+30x430x310010x1+60x2+50+x3+60+x420x5806+x1+1+x2+3x3+7+x49xi{0,1}i=1,,5 (a) Write the LP relaxation of the above model. (b) Get the optimal objective function value of the L.P relaxation frotn Table 1. Is it a lower or an. upper botud? Explain. (c) Is x=[1,0,0,0,1]T a feasible solution to the above problen. If yes, then obtain its objective function value from Table 1. Is it a kower or an upper boumd? Explain. Solve the above problem wsing branch \& bound method, and bexild the euumeration tree using the following strategies. You can use the information from Table 1. Note: Generate ene tree for Pert (d), one for Part (e) and one for Part (f). Draw inside cach nodc, the node number. Neat to each node write objective function nuhe and all the froctional cariables. Draa the branch doun (or bounds) on the left side, and the branch up (or ) bounds on the right aide. While gencnating the tres, you should follow the strategies as deseribed. During the erecution of any strutegy, if the namber of nodes processed is greater than or cyual to 20 , then you can terminate the strulegy. Riport the incambent solution. Alvo, say in percentage, how far it is from the best possible solution. For Strategy-1, write the LP formulation that was soleed at every 5th node- (d) Strategy-1: - Node Selection: Best First Select the node with the best objective function value. - Variable Sebection: Nearest to integer A fructional variable with fractional value nearest to an integer will be used for branching- - Branching Direction: Up Select the branch of side (lower bound is increasod.) (e) Strategy-2: - Node Selection: Depth First the Best Back Select the most recently created child node to solve. If no child exists, then backtrack to the best bound node awalsble in the eatire tree. - Variable Selection: Lowest fraction A fractional variable with lowest fraction will be used for brapching- - Branchaing Direction: Down Select the branch of side (upper bound is decreased.) (f) Strategy-3: - Node Selectiot: Breadth Finst the Best Next All nodes at one level of the search tree are processed before any uode at a deeper hevel. In a given level, best node should be processed first. - Variable Selection: Highest fraction A fractional variable with highest fraction will be used for branching. - Branching Direction: You are froe to piok any rule. Thhk It Optimal Solutions for NII LP Relasetions, if Indicates Table 1 - continued from previous page Thhle 1