Questions posted in the last picture.

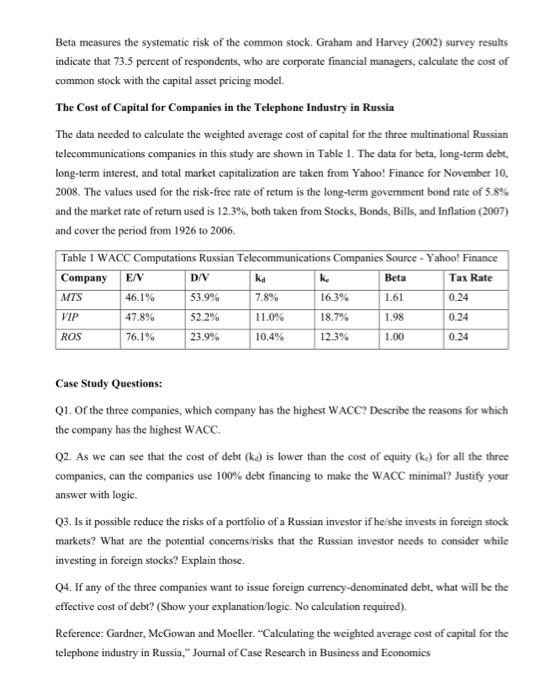
Case Study 2: Cost of capital for the telephone industry in Russia The goal of this paper is to demonstrate how to compute the weighted average cost of capital for companies in an emerging market, specifically, fims in the telephone and oil industries in Russia which is an emerging market. Only systematic risk is priced in the capital asset pricing model. Systematic risk reflects the covariation between returns on the investment and returns on the market portfolio. Markowitz (1952) demonstrates the advantage of portfolio diversification by showing that a portfolio of assets that have less than perfect, positive correlation will have a variance that is less than the average variance of the assets in the portfolio. In fact, if two assets have perfect negative correlation, a portfolio can be constructed that has zero variance. Later, Grubel (1968) shows the gains from international diversification in a two country and two asset environment. An investor can purchase assets in each of the two countries to construct a portfolio in order to create a portfolio that has lower variance. The total effect of portfolio diversification increases as the covariation between returns on an investment and retums on the market decreases, that is, the gains from international diversification are greater when the stock markets between two countries are less correlated. Stock market segmentation leads to increased gains from international diversification because segmented stock markets have lower covariances with respect to each other. Differences in trading costs, information availability, generally accepted accounting principles, legal and political systems, taxes rates, investor expectations and preferences, and government restrictions on stock ownership create barriers to the free flow of capital that cause stock market segmentation for examples see Errunza and Losq (1985), Errunza, Losq, and Padmanabhan (1992), and Bekaert and Harvey (1998). Butler and Joaquin (1998) develop a model of political risk that shows the impact of political risk on the cost of capital for an investment. In the Butler-Joaquin model, the impact of a political risk shock on the cost of capital of the investment depends on the impact of the political risk shock on the expected return of the investment and the covariance of the return on the investment and the return on the market. If the expected impact of a change in the political environment has a negative impaet on expected future cash flows and the covariance between the cash flows from the investment and the return on the market is negative (positive), the effect of a political risk shock is to increase (decrease) the cost of capital for the investment. If the expected impact of a change in the political environment has a positive impact on expected future cash flows and the covariance between the cash flows from the investment and the return on the market is positive (negative), the effect of a political risk shock is to increase (decrease) the cost of capital for the investment. The impact of a political risk shock is dependent on the impact that shock has on the expected rate of return and the covariance of the return on the investment and the return on the market. Standard and Poor's Emerging Stock Market Factbook 2007 shows that US equity markets represented 48.9% of total world stock market capitalization in 1997 and 35.8% of total world stock market capitalization in 2006. However, the market eapitalization of non-US equity markets rose from $11.3 trillion in 1997 to $19.5 trillion in 2006. Although segmentation of global stock markets still exists, globalization has increased over the last twenty years. Computing the Weighted Average Cost of Capital Maximizing the value of the firm is accomplished by investing in projects that have a positive net present value (NPV). The NPV is the discounted present value of the cash flows from the project using the required rate of return. The required rate of return is the weighted average cost of capital and is the opportunity cost of funds for the investor. Modigliani and Miller (1958) show that the required rate of return is the market value weighted average of the costs of each of the forms of capital in the capital structure. The capital structure includes long-term debt and common stock. The weights are determined using the market value of the long-term debt and the common stock. The cost of long-term debt is the yield to maturity of outstanding long-term debt the cost of equity is the rate of retum on outstanding common stock. kwacc=D/kd(1t)+E/V(kt) where, kwacc - the firms overage weighted average cost of capital D. V - the proportion of debt in the capital structure E/V - the weight for common stock in the capital structure Kd - marginal cost of debt t- marginal tax rate Modigliani and Miller (1958) assume that there that taxes do no exist. In the current world, the cost of long-term debt is adjusted for taxes and the cost of common stock is not adjusted for taxes. The weights for long-term debt and common stock are based on total market values of long-term debt and common stock. The weight for the debt component of the capital structure is the total market value of the debt divided by the total market value of the firm. The weight for the common stock equity component of the capital structure is the total market value of the common stock equity divided by the total market value of the firm. The cost of the long-term debt is the yield to maturity of outstanding bonds and is equal to interest rate that equates the current price and the expected future cash flows from the coupon payments and the maturity value of the bonds. Po=CPt/(1+kd)t+FV/(1+kd)T where, Po - the current price of the outstanding bond CPt - the coupon payment of the bond FV - the maturity value of the bond T - the time to maturity The yield to maturity is the discount rate that equates the current price and the expected values of the coupon payments and the maturity value of the bonds. The cost of common stock equity is computed using security market line Sharpe (1964). The cost of common stock is the risk free rate of retum plus the risk premium. The risk premium is beta for the stock times the market price of risk, the expected return for the market minus the risk free rate. kc=kr+(kmk1) where, ke the component cost of common stock equity kmin - the expected rate of return on the market kf - the risk free rate of return - the beta of the common stock equity Beta measures the systematic risk of the common stock. Graham and Harvey (2002) survey results indicate that 73.5 percent of respondents, who are corporate financial managers, calculate the cost of common stock with the capital asset pricing model. The Cost of Capital for Companies in the Telephone Industry in Russia The data needed to calculate the weighted average cost of capital for the three multinational Russian telecommunications companies in this study are shown in Table 1. The data for beta, long-term debt, long-term interest, and total market capitalization are taken from Yahoo! Finance for November 10 , 2008. The values used for the risk-free rate of retum is the long-term govermment bond rate of 5.8% and the market rate of return used is 12.3\%, both taken from Stocks, Bonds, Bills, and Inflation (2007) and cover the period from 1926 to 2006. Case Study Questions: Q1. Of the three companies, which company has the highest WACC? Describe the reasons for which the company has the highest WACC. Q2. As we can see that the cost of debt (kd) is lower than the cost of equity ( ke) for all the three companies, can the companies use 100% debt financing to make the WACC minimal? Justify your answer with logic. Q3. Is it possible reduce the risks of a portfolio of a Russian investor if he/she invests in foreign stock markets? What are the potential concerns/risks that the Russian investor needs to consider while investing in foreign stocks? Explain those. Q4. If any of the three companies want to issue foreign currency-denominated debt, what will be the effective cost of debt? (Show your explanation/logic. No calculation required). Reference: Gardner, McGowan and Moeller. "Calculating the weighted average cost of capital for the telephone industry in Russia," Journal of Case Research in Business and Economics Case Study 2: Cost of capital for the telephone industry in Russia The goal of this paper is to demonstrate how to compute the weighted average cost of capital for companies in an emerging market, specifically, fims in the telephone and oil industries in Russia which is an emerging market. Only systematic risk is priced in the capital asset pricing model. Systematic risk reflects the covariation between returns on the investment and returns on the market portfolio. Markowitz (1952) demonstrates the advantage of portfolio diversification by showing that a portfolio of assets that have less than perfect, positive correlation will have a variance that is less than the average variance of the assets in the portfolio. In fact, if two assets have perfect negative correlation, a portfolio can be constructed that has zero variance. Later, Grubel (1968) shows the gains from international diversification in a two country and two asset environment. An investor can purchase assets in each of the two countries to construct a portfolio in order to create a portfolio that has lower variance. The total effect of portfolio diversification increases as the covariation between returns on an investment and retums on the market decreases, that is, the gains from international diversification are greater when the stock markets between two countries are less correlated. Stock market segmentation leads to increased gains from international diversification because segmented stock markets have lower covariances with respect to each other. Differences in trading costs, information availability, generally accepted accounting principles, legal and political systems, taxes rates, investor expectations and preferences, and government restrictions on stock ownership create barriers to the free flow of capital that cause stock market segmentation for examples see Errunza and Losq (1985), Errunza, Losq, and Padmanabhan (1992), and Bekaert and Harvey (1998). Butler and Joaquin (1998) develop a model of political risk that shows the impact of political risk on the cost of capital for an investment. In the Butler-Joaquin model, the impact of a political risk shock on the cost of capital of the investment depends on the impact of the political risk shock on the expected return of the investment and the covariance of the return on the investment and the return on the market. If the expected impact of a change in the political environment has a negative impaet on expected future cash flows and the covariance between the cash flows from the investment and the return on the market is negative (positive), the effect of a political risk shock is to increase (decrease) the cost of capital for the investment. If the expected impact of a change in the political environment has a positive impact on expected future cash flows and the covariance between the cash flows from the investment and the return on the market is positive (negative), the effect of a political risk shock is to increase (decrease) the cost of capital for the investment. The impact of a political risk shock is dependent on the impact that shock has on the expected rate of return and the covariance of the return on the investment and the return on the market. Standard and Poor's Emerging Stock Market Factbook 2007 shows that US equity markets represented 48.9% of total world stock market capitalization in 1997 and 35.8% of total world stock market capitalization in 2006. However, the market eapitalization of non-US equity markets rose from $11.3 trillion in 1997 to $19.5 trillion in 2006. Although segmentation of global stock markets still exists, globalization has increased over the last twenty years. Computing the Weighted Average Cost of Capital Maximizing the value of the firm is accomplished by investing in projects that have a positive net present value (NPV). The NPV is the discounted present value of the cash flows from the project using the required rate of return. The required rate of return is the weighted average cost of capital and is the opportunity cost of funds for the investor. Modigliani and Miller (1958) show that the required rate of return is the market value weighted average of the costs of each of the forms of capital in the capital structure. The capital structure includes long-term debt and common stock. The weights are determined using the market value of the long-term debt and the common stock. The cost of long-term debt is the yield to maturity of outstanding long-term debt the cost of equity is the rate of retum on outstanding common stock. kwacc=D/kd(1t)+E/V(kt) where, kwacc - the firms overage weighted average cost of capital D. V - the proportion of debt in the capital structure E/V - the weight for common stock in the capital structure Kd - marginal cost of debt t- marginal tax rate Modigliani and Miller (1958) assume that there that taxes do no exist. In the current world, the cost of long-term debt is adjusted for taxes and the cost of common stock is not adjusted for taxes. The weights for long-term debt and common stock are based on total market values of long-term debt and common stock. The weight for the debt component of the capital structure is the total market value of the debt divided by the total market value of the firm. The weight for the common stock equity component of the capital structure is the total market value of the common stock equity divided by the total market value of the firm. The cost of the long-term debt is the yield to maturity of outstanding bonds and is equal to interest rate that equates the current price and the expected future cash flows from the coupon payments and the maturity value of the bonds. Po=CPt/(1+kd)t+FV/(1+kd)T where, Po - the current price of the outstanding bond CPt - the coupon payment of the bond FV - the maturity value of the bond T - the time to maturity The yield to maturity is the discount rate that equates the current price and the expected values of the coupon payments and the maturity value of the bonds. The cost of common stock equity is computed using security market line Sharpe (1964). The cost of common stock is the risk free rate of retum plus the risk premium. The risk premium is beta for the stock times the market price of risk, the expected return for the market minus the risk free rate. kc=kr+(kmk1) where, ke the component cost of common stock equity kmin - the expected rate of return on the market kf - the risk free rate of return - the beta of the common stock equity Beta measures the systematic risk of the common stock. Graham and Harvey (2002) survey results indicate that 73.5 percent of respondents, who are corporate financial managers, calculate the cost of common stock with the capital asset pricing model. The Cost of Capital for Companies in the Telephone Industry in Russia The data needed to calculate the weighted average cost of capital for the three multinational Russian telecommunications companies in this study are shown in Table 1. The data for beta, long-term debt, long-term interest, and total market capitalization are taken from Yahoo! Finance for November 10 , 2008. The values used for the risk-free rate of retum is the long-term govermment bond rate of 5.8% and the market rate of return used is 12.3\%, both taken from Stocks, Bonds, Bills, and Inflation (2007) and cover the period from 1926 to 2006. Case Study Questions: Q1. Of the three companies, which company has the highest WACC? Describe the reasons for which the company has the highest WACC. Q2. As we can see that the cost of debt (kd) is lower than the cost of equity ( ke) for all the three companies, can the companies use 100% debt financing to make the WACC minimal? Justify your answer with logic. Q3. Is it possible reduce the risks of a portfolio of a Russian investor if he/she invests in foreign stock markets? What are the potential concerns/risks that the Russian investor needs to consider while investing in foreign stocks? Explain those. Q4. If any of the three companies want to issue foreign currency-denominated debt, what will be the effective cost of debt? (Show your explanation/logic. No calculation required). Reference: Gardner, McGowan and Moeller. "Calculating the weighted average cost of capital for the telephone industry in Russia," Journal of Case Research in Business and Economics