Reed solomon codes questions

1. Recall that R-S of dimension (number of coefs) k = 2 and length (number of evals) n = 4 corrects t = 1 error. The slogan "there is a unique line through >= 3 received points" suggests an algorithm. Recall. Then encode, make one error, swap with a neighbor, and decode the neighbor's received word.

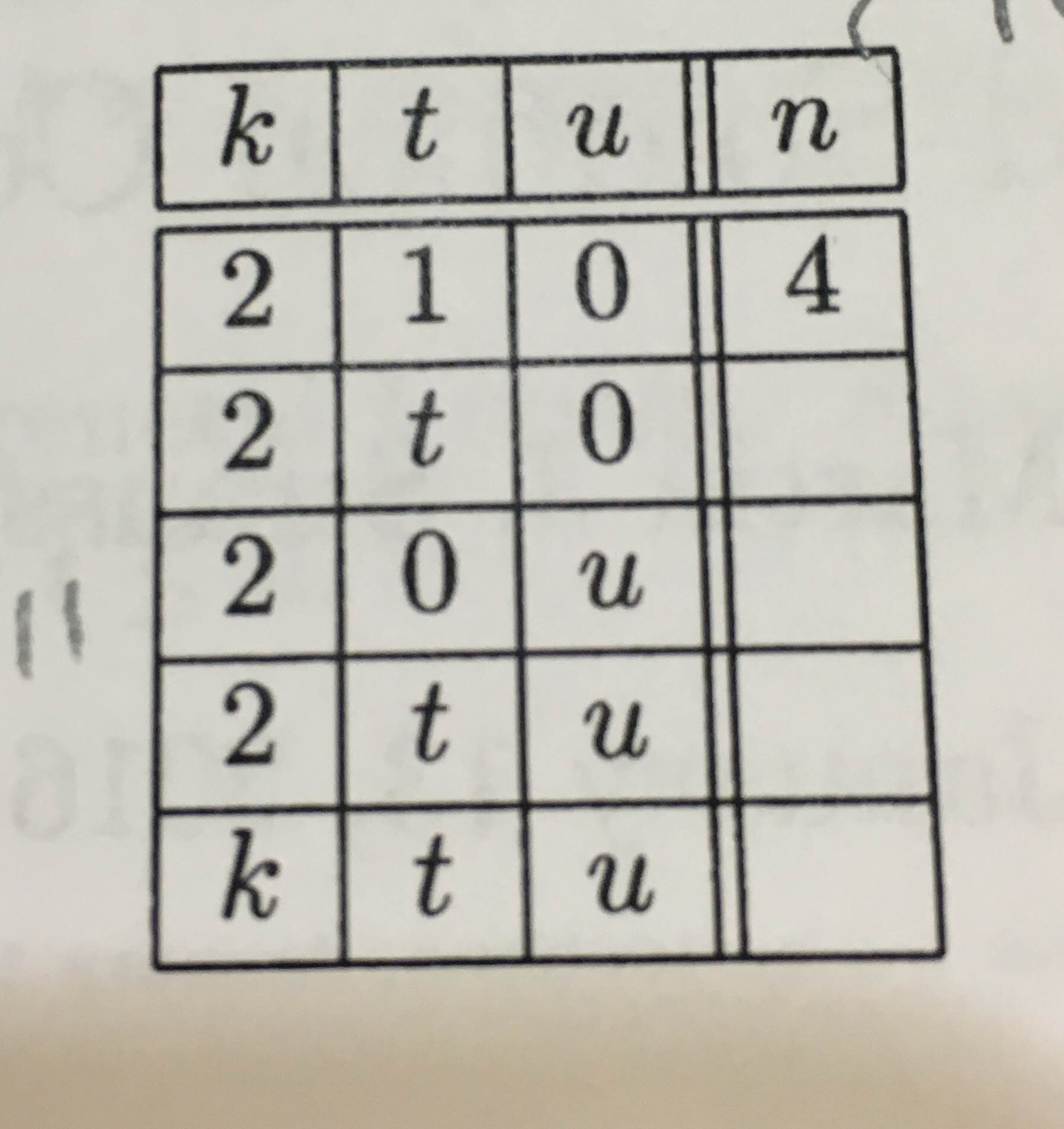
2. Suppose there are t errors and u (other) erasures, simultaneously, in the channel, and the client specifies k. What is the minimum value for n that works?

(If you can more easily find a sufficiently large value for n, even if it's not optimal, that's valuable, too. To find least n, show that n works and n-1 doesn't work.)

Fill in this table (in row order is suggested), building toward n as a function of k,t, u. Draw points! Draw lines! draw quadratics!

-- please explain in detail :( I don't understand this question answer.