Answered step by step
Verified Expert Solution
Question
1 Approved Answer
signed area under the curve between 0 and x. Note that on the left-hand side of the =, the variable is .x. The on
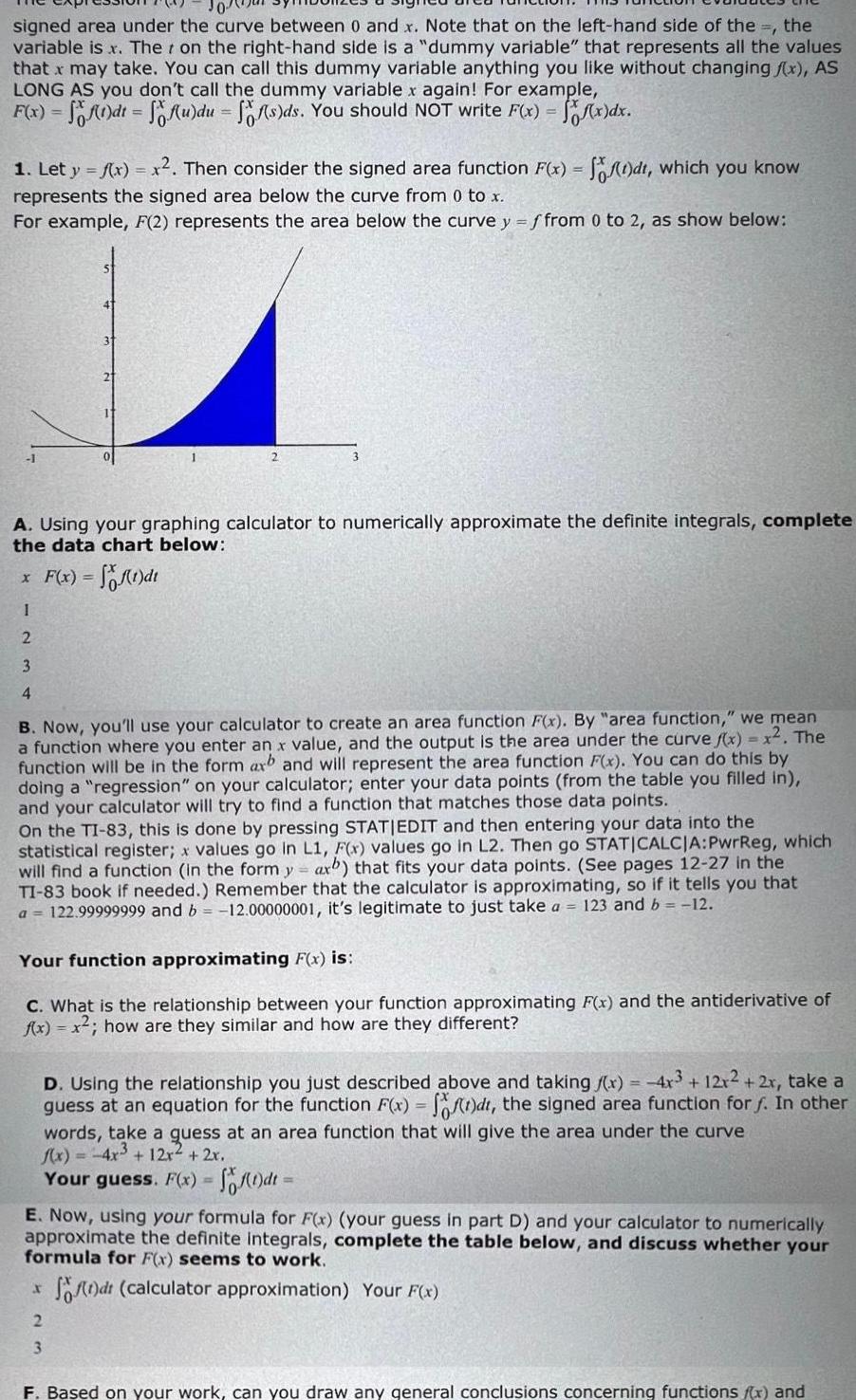
signed area under the curve between 0 and x. Note that on the left-hand side of the =, the variable is .x. The on the right-hand side is a "dummy variable" that represents all the values that x may take. You can call this dummy variable anything you like without changing f(x), AS LONG AS you don't call the dummy variable x again! For example, F(x)-dt-udu -Rs)ds. You should NOT write Fix)-f)dx. = = = 1. Let y = f(x) = x. Then consider the signed area function F(x) = f(dt, which you know represents the signed area below the curve from 0 to x. For example, F(2) represents the area below the curve y = f from 0 to 2, as show below: -1 31 3 A. Using your graphing calculator to numerically approximate the definite integrals, complete the data chart below: x F(x) = di 1 2 3 4 == B. Now, you'll use your calculator to create an area function F(x). By "area function," we mean a function where you enter an x value, and the output is the area under the curve f(x) = x. The function will be in the form arb and will represent the area function F(x). You can do this by doing a "regression" on your calculator; enter your data points (from the table you filled in), and your calculator will try to find a function that matches those data points. On the TI-83, this is done by pressing STATIEDIT and then entering your data into the statistical register; x values go in L1, F(x) values go in L2. Then go STAT|CALCIA: PwrReg, which will find a function (in the form y axb) that fits your data points. (See pages 12-27 in the TI-83 book if needed.) Remember that the calculator is approximating, so if it tells you that a = 122.99999999 and b = -12.00000001, it's legitimate to just take a = 123 and b = -12. Your function approximating F(x) is: C. What is the relationship between your function approximating F(x) and the antiderivative of f(x) = x; how are they similar and how are they different? = D. Using the relationship you just described above and taking f(x)--4x3 + 12x2+2x, take a guess at an equation for the function F(x) -fd, the signed area function for f. In other words, take a quess at an area function that will give the area under the curve f(x)=-4x3 + 12x + 2x. Your guess. F(x)=(1)dt= E. Now, using your formula for F(x) (your guess in part D) and your calculator to numerically approximate the definite integrals, complete the table below, and discuss whether your formula for F(x) seems to work. I dt (calculator approximation) Your F(x) 2 3 F. Based on your work, can you draw any general conclusions concerning functions f(x) and
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


