solve the answers handwritten but please type all the final answers together in the different section after solving. Thanks.

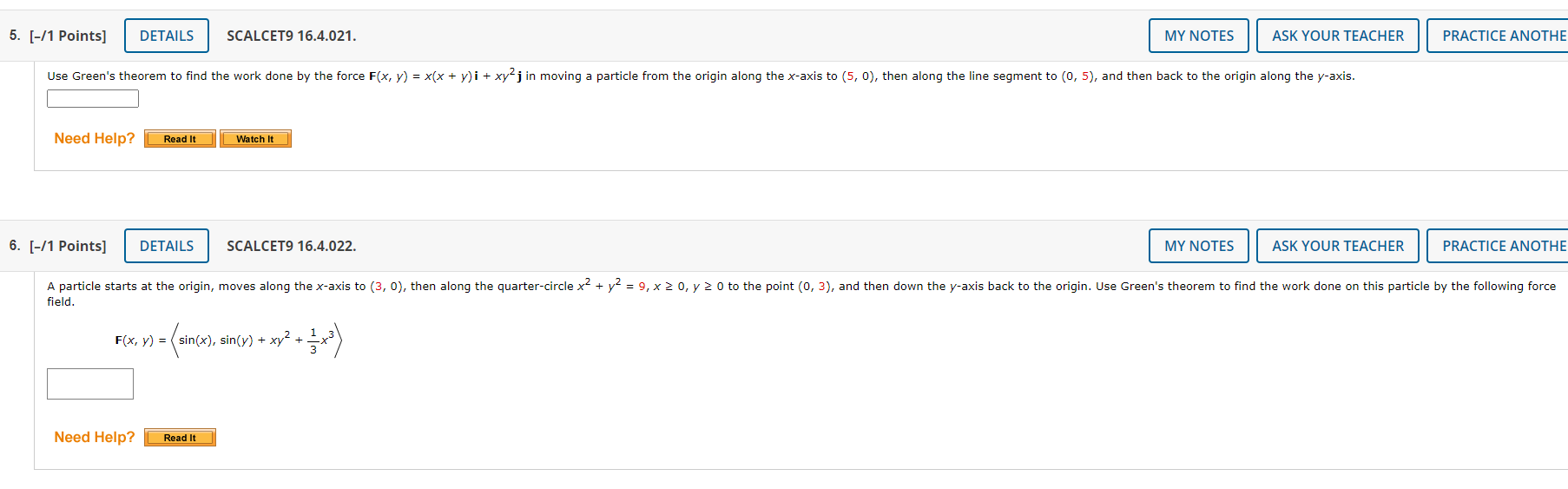
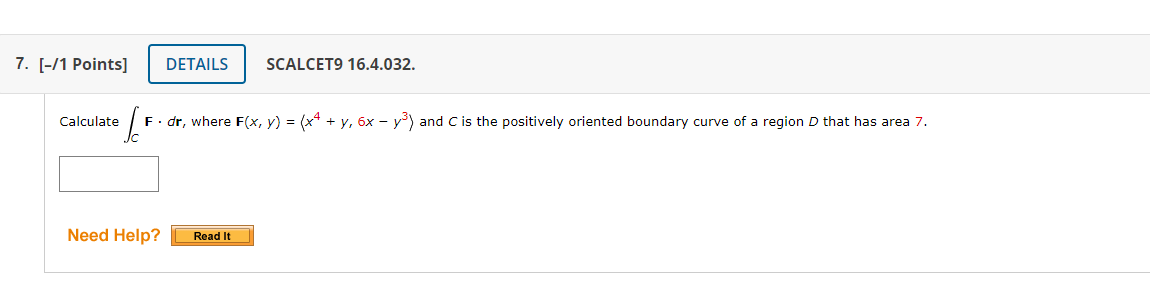
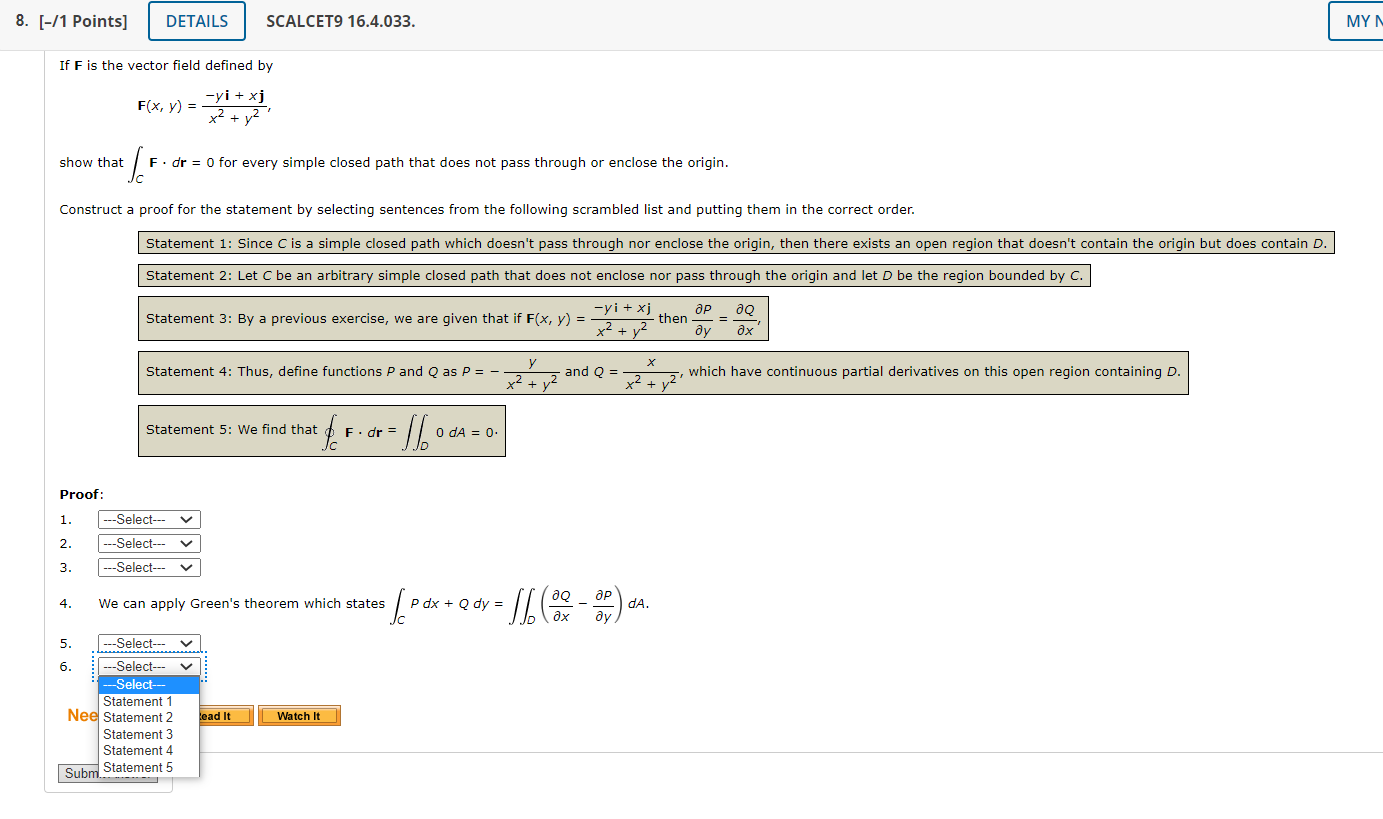
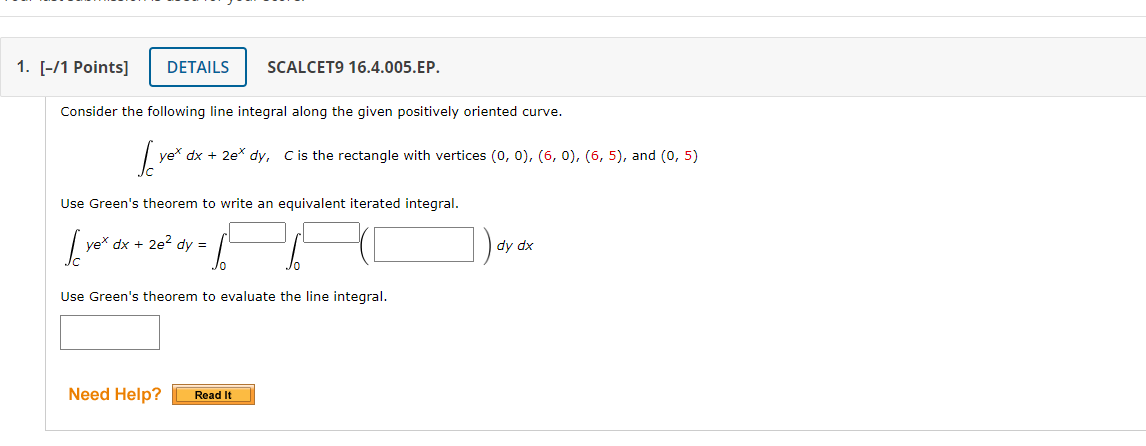
1. [-/1 Points] DETAILS SCALCET9 16.4.005.EP. Consider the following line integral along the given positively oriented curve. ye dx + 2e* dy, C is the rectangle with vertices (0, 0), (6, 0), (6, 5), and (0, 5) Use Green's theorem to write an equivalent iterated integral. ye* dx + 2e2 dy = dy dx Use Green's theorem to evaluate the line integral. Need Help? Read It3. [-/1 Points] DETAILS SCALCET9 16.4.011. Use Green's theorem to evaluate the line integral along the given positively oriented curve. 9y3 dx - 9x3 dy, C is the circle x2 + y2 = 4 Need Help? Read It Watch It 4. [-/1 Points] DETAILS SCALCET9 16.4.015.EP. Consider F . dr given the following. F(x, y) = (y cos(x) - xy sin(x), xy + x cos(x)), C is the triangle from (0, 0) to (0, 12) to (3, 0) to (0, 0) Use Green's Theorem to write an equivalent iterated integral. (Check the orientation of the curve before applying the theorem.) F . ar = [/([ dy dx A : B Use Green's Theorem to evaluate the line integral. Need Help? Read It5. [-/1 Points] DETAILS SCALCET9 16.4.021. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHE Use Green's theorem to find the work done by the force F(x, y) = x(x + y) i + xy j in moving a particle from the origin along the x-axis to (5, 0), then along the line segment to (0, 5), and then back to the origin along the y-axis. Need Help? Read It Watch It 6. [-/1 Points] DETAILS SCALCET9 16.4.022. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHE A particle starts at the origin, moves along the x-axis to (3, 0), then along the quarter-circle x2 + yz = 9, x 2 0, y 2 0 to the point (0, 3), and then down the y-axis back to the origin. Use Green's theorem to find the work done on this particle by the following force field F(x, y) = sin(x), sin(y) + xy2 + 1x3) Need Help? Read It7. [-/1 Points] DETAILS SCALCET9 16.4.032. Calculate F . dr, where F(x, y) = (x# + y, 6x - y') and C is the positively oriented boundary curve of a region D that has area 7. Need Help? Read It8. [-/1 Points] DETAILS SCALCET9 16.4.033. MY N If F is the vector field defined by F(x, y ) = _yl+ xj show that F . dr = 0 for every simple closed path that does not pass through or enclose the origin. c Construct a proof for the statement by selecting sentences from the following scrambled list and putting them in the correct order. Statement 1: Since C is a simple closed path which doesn't pass through nor enclose the origin, then there exists an open region that doesn't contain the origin but does contain D. Statement 2: Let C be an arbitrary simple closed path that does not enclose nor pass through the origin and let D be the region bounded by C. Statement 3: By a previous exercise, we are given that if F(x, y) = - -yi+xj - then OP aQ * 2 + 12 ay dx X Statement 4: Thus, define functions P and Q as P = - y *2 + 1/2 and Q = - 2 + 12, which have continuous partial derivatives on this open region containing D. Statement 5: We find that f F . or = / / o dA = 0. Proof: 1. ---Select--- 2. --Select--- 3. ---Select-- We can apply Green's theorem which states / pox + Q dy = / / aQ ap ax ay dA . 5. ---Select-- 6. ---Select--- :.... -Select-- Statement 1 Nee Statement 2 ead It Watch It Statement 3 Statement 4 Subm. Statement 52. [-/1 Points] DETAILS SCALCET9 16.4.009.MI. Use Green's theorem to evaluate the line integral along the given positively oriented curve. (3y + 7evx) dx + (8x + 3 cos(y-)) dy, C is the boundary of the region enclosed by the parabolas y = x2 and x = y2 Need Help? Read It Watch It Master It