Solve the following problem using MATLAB. The yield stress of many metals, 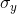, varies with the size of the grains. Often, the relationship between the grain size, d, and the yield stress is modeled with the Hall-Petch equation: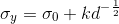

The following are results from measurements of average grain size and yield stress:

(a) Determine the constants 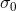and k such that the Hall-Petch equation will best fit the data. Plot the data points (circle markers) and the Hall-Petch equation as a solid line. Use the Hall-Petch equation to estimate the yield stress of a specimen with a grain size of 0.003 mm. (b) Find the quadratic function that best fits the data by writing a MATLAB user-defined function that determines the coefficients of a quadratic polynomial, f(x) = a₂x² + a₁x + a₀, that best fits a given set of data points. Name the function a= QuadFit(x,y), where the input arguments x and y are vectors with the coordinates of the data points, and the output argument a is a three-element vector with the values of the coefficients a₂, a₁ and a₀. Plot the data points (circle markers) and the quadratic equation as a solid line. Use the quadratic equation to estimate the yield stress of a specimen with a grain size of 0.003 mm.