Solving 9.17!! Can someone help me develop an m-file based on Figure 9.5 (attached below) to implement Gauss elimination with partial pivoting? I need to complete problem 9.17 below, which involves working with the function from Figure 9.5 and modifying it.

9.17 Develop an M-file function based on Fig. 9.5 to im plement Gauss elimination with partial pivoting. Modify the function so that it computes and returns the determinant (with the correct sign), and detects whether the system is sin- gular based on a near-zero determinant. For the latter, define near-zero as being when the absolute value of the determi- nant is below a tolerance. When this occurs, design the func- tion so that an error message is displayed and the function terminates. Here is the functions first line: function [x, D] = GaussPivotNew(A, b, tol) where D the determinant and tol = the tolerance. Test your program for Prob. 9.5 with tol-1 10-5.

We then have to test it using problem 9.5 where D = determinant, and tolerance = 1 x 10^(-5). Please help, many thanks!!! :)

This is all the same problem, but one image is the Figure from the text needed, and the other is problem 9.5 since we have ti use that info to solve 9.17. Thanks!!

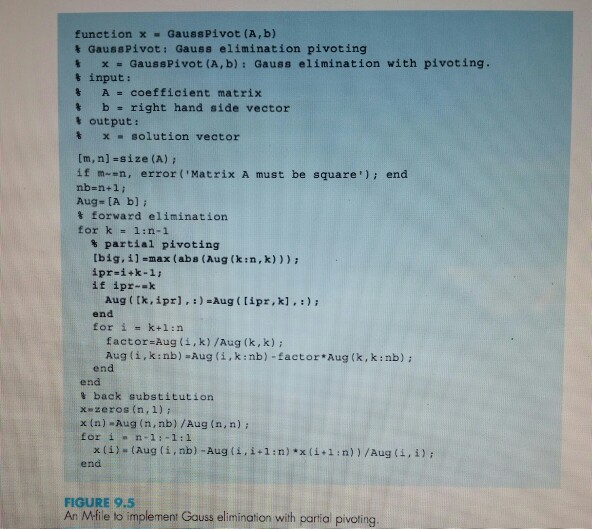
9.17 Develop an M-file function based on Fig. 9.5 to im plement Gauss elimination with partial pivoting. Modify the function so that it computes and returns the determinant (with the correct sign), and detects whether the system is sin- gular based on a near-zero determinant. For the latter, define "near-zero" as being when the absolute value of the determi- nant is below a tolerance. When this occurs, design the func- tion so that an error message is displayed and the function terminates. Here is the functions first line: function [x, D] = GaussPivotNew(A, b, tol) where D the determinant and tol = the tolerance. Test your program for Prob. 9.5 with tol-1 10-5