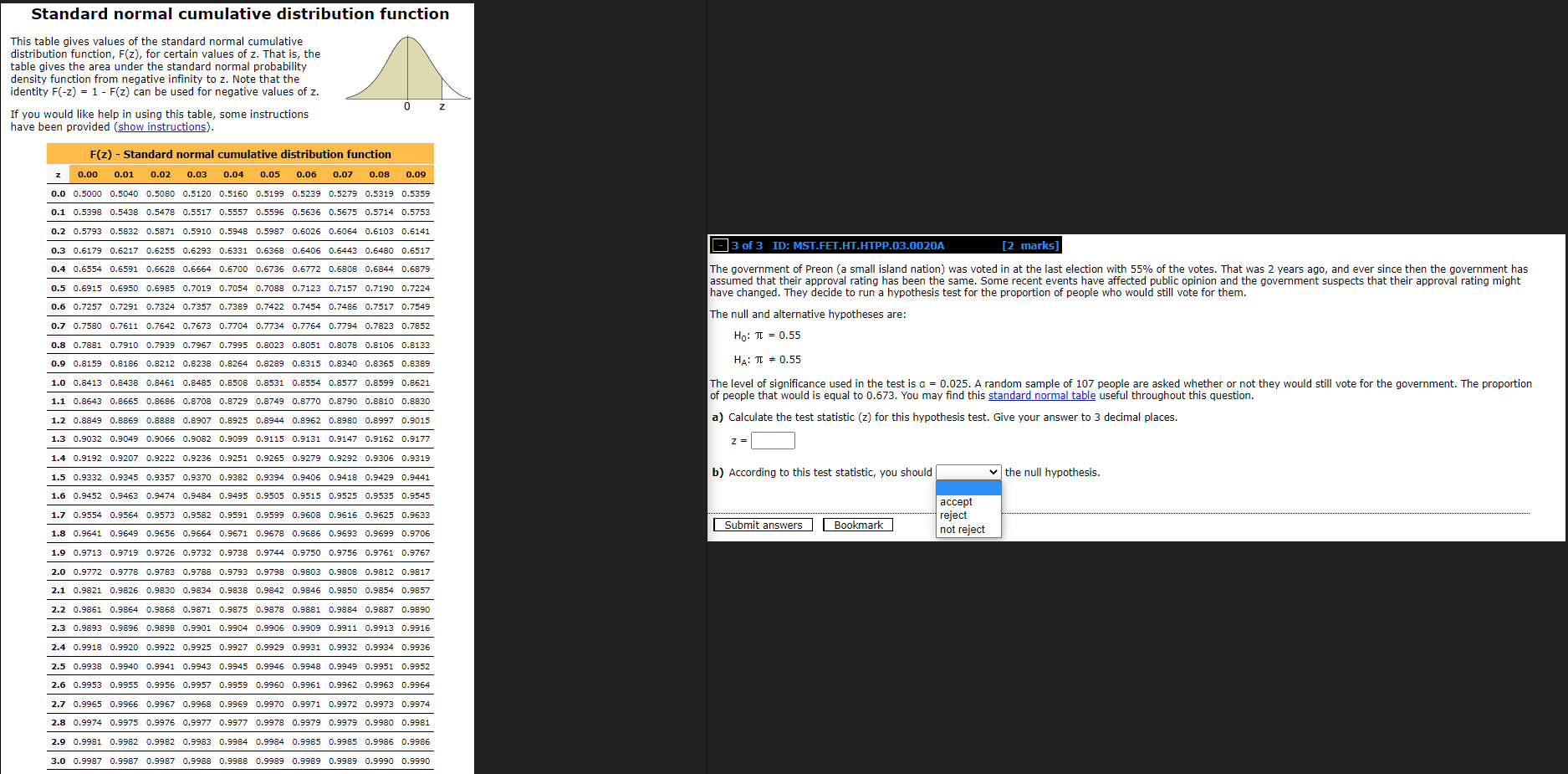
Standard normal cumulative distribution function This table gives values of the standard normal cumulative distribution function, F(z), for certain values of z. That is, the table gives the area under the standard normal probability density function from negative infinity to z. Note that the identity F(-z) = 1 - F(z) can be used for negative values of z. 0 If you would like help in using this table, some instructions have been provided (show instructions). F(z) - Standard normal cumulative distribution function 2 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.5000 0.5040 0.5080 0. 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359 0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753 0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141 0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 3 of 3 ID: MST.FET.HT.HTPP.03.0020A [2 marks] 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879 The government of Preon (a small island nation) was voted in at the last election with 55% of the votes. That was 2 years ago, and ever since then the government has 0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224 assumed that their approval rating has been the same. Some recent events have affected public opinion and the government suspects that their approval rating might have changed. They decide to run a hypothesis test for the proportion of people who would still vote for them. 0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549 The null and alternative hypotheses are: 0.7 0.7580 0.7611 0.7642 0.7673 3 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852 Ho: TI = 0.55 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133 0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 0.8340 0.8365 0.8389 HA: TI = 0.55 1.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621 The level of significance used in the test is a = 0.025. A random sample of 107 people are asked whether or not they would still vote for the government. The proportion .1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830 of people that would is equal to 0.673. You may find this standard normal table useful throughout this question. 1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015 a) Calculate the test statistic (z) for this hypothesis test. Give your answer to 3 decimal places. 1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 Z = 1.4 0.9192 0.9207 0.9222 0.9236 0.9251 5 0.9279 0.9292 0.9306 0.9319 1.5 0.9332 0 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.9441 b) According to this test statistic, you should the null hypothesis. 1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0 0.9525 0.9535 0.9545 accept 1.7 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633 reject 1.8 0.9641 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706 Submit answers Bookmark not reject 1.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.9744 4 0.9750 0.9756 0.9761 0.9767 2.0 0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817 2.1 0.9821 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850 0.9854 0.9857 2.2 0.9861 0. 0.9864 0.9868 0.9871 0.9875 0.9878 8 0.9881 0.9884 0.9887 0.9890 2.3 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9916 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932 0.9934 0 2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952 2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964 2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0 0.9971 0.9972 0.9973 0.9974 2.8 0.9974 0.9975 0.9977 0.9977 0.9978 0 0.9979 0.9980 0.9981 2.9 0.9981 0.9982 0.9982 0.9983 0.9984 0.9984 4 0.9985 0.9985 0.9986 0.9986 3.0 0.9987 0.9987 0.9987 0.9988 0.9988 0.9989 0.9989 0.9989 0.9990 0.9990