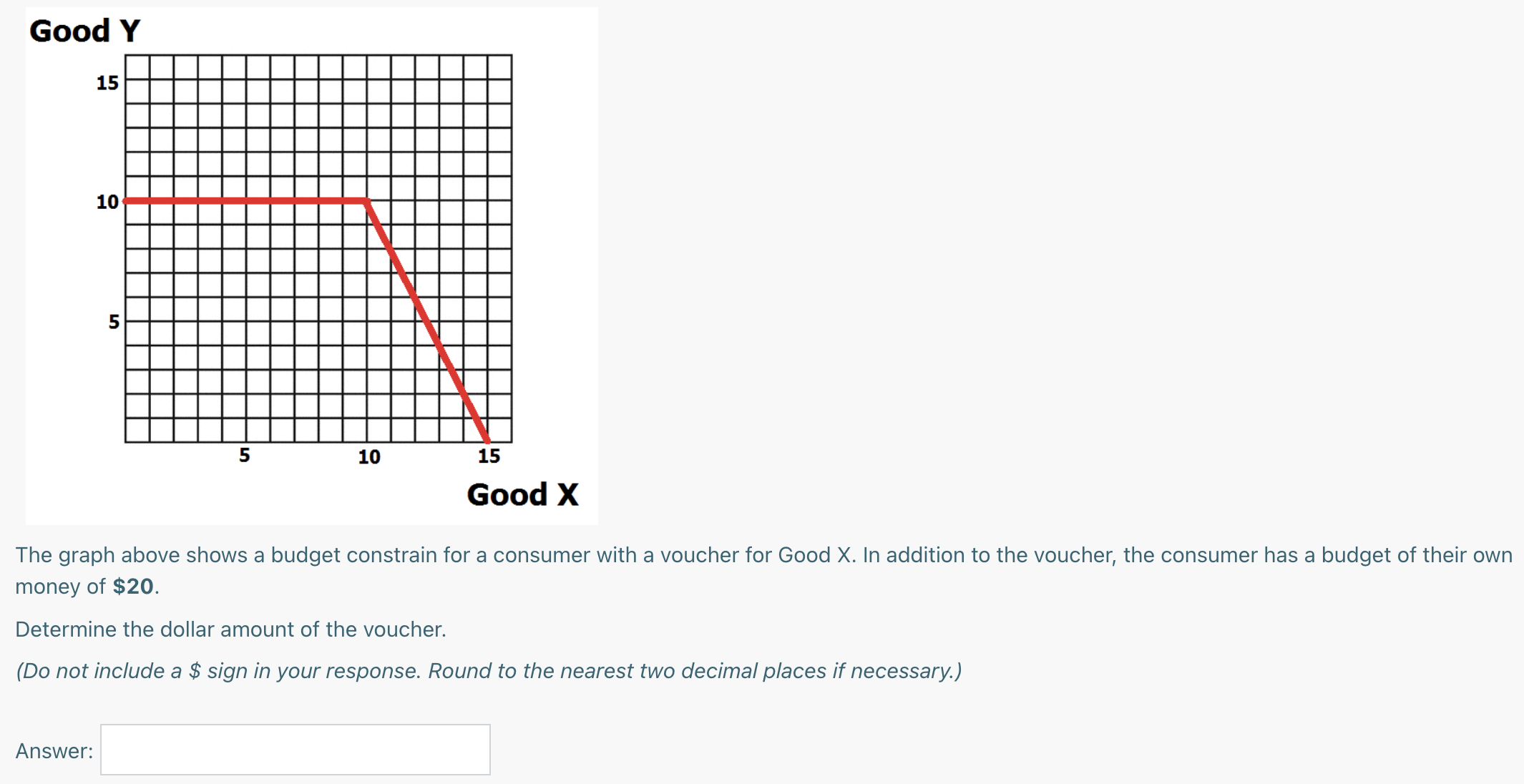
Suppose that a consumer had a utility function given by: U=XY3. This consumer has a budget of $48. Fill in the value of this consumer's demand function. X = * (1/PX) . (For instance, if X = 4/Px, then X = 4 * (1/Px) and enter 4)Suppose that Jim uses his budget to purchase 100 units of Good X and 100 units of Good Y. When the price of Good X rises, he purchases 50 units of Good X and 95 units of Good Y. An economist calculates his compensated budget and finds that in that scenario, Jim would buy 80 units of Good X and 105 units of Good Y. Calculate the income effect. (Remember to include a negative sign (-) if the effect reduces the quantity.) Answer: Suppose that Jim uses his budget to purchase 100 units of Good X and 100 units of Good Y. When the price of Good X rises, he purchases 70 units of Good X and 95 units of Good Y. An economist calculates his compensated budget and finds that in that scenario, Jim would buy 80 units of Good X and 105 units of Good Y. Calculate the substitution effect. (Remember to include a negative sign () if the effect reduces the quantity.) Answer: Suppose that a consumer had a budget of $14 to spend on Good X and Good Y. The price of Good X is $5 and the price of Good Y is $2. The store selling Good X is offer a deal where you can buy one unit of Good X and get the next unit of Good X that you buy for 40% of the original price. Determine the X-intercept of the budget line for the consumer in this situation. Answer: Suppose that a there are two goods, X and Y. The price of Good X is $5 and the price of Good Y is $10. The seller of Good X offers a deal where if a consumer buys 1 unit of Good X they pay full price, but the second unit of Good X is only $3. Calculate the slope of the budget constraint between 1 unit of Good X and 2 units of Good X. (Remember to include a negative sign. Round to the nearest two decimal places if necessary.) Answer: The graph above shows a budget constrain for a consumer with a voucher for Good X. In addition to the voucher, the consumer has a budget of their own money of $20. Determine the dollar amount of the voucher. (Do not include a $ sign in your response. Round to the nearest two decimal places if necessary.) Answer: Suppose the market was made up of two demanders. Demander 1 has a demand function given by: on) = 100 - 2P. Demander 2 has a demand function given by: qD = 250 - 4P. The horizontal summation of these two demand functions will, when graphed, have a kink (point where the slope changes). Determine the price associated with the kink in the total demand function. (Do not include a dollar sign in your response. Round to the nearest 2 decimal places if necessary.) Answer: Suppose the total demand function for a good was made up of 20 identical, individual demanders all with a demand function given by: (1:, = 20 - 0.5P. Find the inverse, total demand function and fill in the missing values below. P = 40 - QD (Round to the nearest two decimal places if necessary.) Suppose the demand for a good was given by: QB: 48 - 4P. Calculate consumer surplus when price is $9. (Do not include a $ sign in your response. Round to the nearest 2 decimal places if necessary.) Answer: Suppose the demand for a good was given by: on = 70 - 2P. Calculate the change in consumer surplus from when the price falls from $19 to $17. (Do not include a dollar sign in your response. Round to the nearest 2 decimal places if necessary.)