Suppose you have a supercomputer that can run jobs one at a time. You have a set of jobs J that you need to run and want to determine the best order in which to run them. Not all jobs take the same amount of time to complete; specically, job jk takes time t_k to complete. Each job must run to completion once started, so you cant pause or stop a job aer starting it. Certain jobs depend on results computed by other jobs, so you cannot run the jobs in a completely arbitrary order. Specically, you have a Directed Acyclic Graph (DAG) G = (J, E) whose nodes are the jobs J and where each edge (Ji_, j_k) indicates that job Ji must be run before job jk. Under these restrictions, its easy to schedule all the jobs as eciently as possible: just topologically sort the DAG and run the jobs in that order. Of course, there is a catch. Associated with each job jk is a cost function cosT_k(t) denoting the cost of completing job j_k at time t. these functions are monotonically increasing, so for any job jk and any > 0, we have cosT_k(t) k(t + ). Your task is to nd a way of ordering all of the jobs on the supercomputer so that all constraints are satised and the total cost is as low as possible. Specically, you want to minimize.

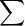cosT_k(f(j_k)). j|kJ

Where f(j_k) denotes the time at which job jk nishes. is a problem is known to be NP-hard. A nave algorithm for this problem is to try out every possible topological ordering of the DAG and nd the ordering with the least total cost, but this algorithm can be incredibly slow

(i) Prove that for all n 0, there is a DAG with n nodes and (n!) topological orderings. is shows the nave algorithm has worst-case runtime(n!). Fortunately, we can improve upon the nave algorithm using dynamic programming. Let us call a set S J a feasible set i for every jk S, if there is a path from Ji to jk in G (i.e., jk depends on ji ), then ji S. Intuitively, a feasible set is a set of jobs that can be scheduled without missing any prerequisites. For example, in the following DAGs, the indicated nodes are feasible sets:

For any feasible set S, let last(S) denote the set of all jobs jk S such that (jk, ji) 6 E for any ji S. In other words, last(S) consists of all jobs in S that no other jobs depend on.

(ii) Prove that if S is a feasible set, then S \ {j} is feasible for any j last(S). For any feasible set S, let opt(S) denote the optimal cost of scheduling the jobs in set S.

(iii) Prove that in an optimal schedule for the jobs in S, the supercomputer is never idle before all jobs have completed (i.e., until all jobs have nished executing, the supercomputer is always executing some job.) (iv) Write a recurrence relation for opt(S), then prove that your recurrence relation is correct.

Given a recurrence relation for OPT(S), it is possible to nd the cost of an optimal schedule by using the following dynamic programming algorithm:

Let DP be a table of size 2n.

For each subset S J, in an appropriate order: If S is feasible, ll in DP[S] based on the recurrence from (iv).

Return DP[J].

If we assume each function costk can be evaluated in time O(1), then (with the right recurrence relation for opt(S) it is possible to ll each entry of DP in time O(n + m). It is also possible to check whether a set is feasible in time O(n + m). is means that the overall runtime for this algorithm is O(2n(n + m)), which is signicantly beer than the (n!) worst-case of the nave algorithm!